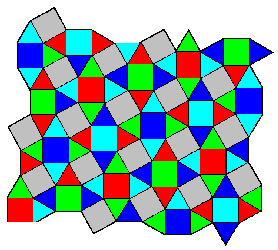
Figure 5
(iv) There is only one precise coloring of (3,3,3,3,6) for which the
hexagons are not all the same color. It is chirally perfect. See Figure
6. There are exactly two precise chirally perfect colorings of (3,3,3,3,6)
in which the hexagons are all the same color. In one of these (Figure 7)
the pairs of triangles at opposite edges of a hexagon are the same color.
In the other (Figure 8) the three triangles at alternate edges of a
hexagon are the same color.
(v) There are infinitely many precise colorings of (3,3,3,4,4). None
are perfect. However, there are exactly eight precise chirally perfect
colorings, of which four reflect into the other four. These four are shown
in Figures 9, 10, 11, 12. It is remarkable that in the last of these all
five colors appear in each strip of squares, whereas in the first three two
colors alternate in each strip.
Some indications of the proof of the theorem follow:
(i) Lemma:
If a 3-valent planar graph (infinite or finite) has a region
with an odd number of edges then it admits no precise coloring. This lemma
is proved by a simple parity argument on the (two) colors of the regions
surrounding the "odd" region. This lemma also rules out any precise
coloring of the regular tetrahedron or regular dodecahedron. (For the same
reason there are no precise colorings of four of the Archimedean polyhedra:
the truncations of the tetrahedron, cube, dodecahedron, and icosahedron.)
(ii) In (4,6,12) and (4,8,8) the three colors at any vertex immediately
force all the colors at all other vertices. Then, in Figure 1, any
isometry takes squares to squares, hexagons to hexagons and dodecagons to
dodecagons. Hence it is the identity permutation of their colors, so the
coloring is perfect. In Figure 2
every rotation about the centers of the octagons is the
identity permutation of the colors. Every quarter-turn about the center
of a square interchanges the two octagon colors; similarly, every
rotation about a mid-edge point interchanges the two octagon colors and
fixes the square color. Likewise, every translation is the identity permutation or
interchanges two colors. Every reflection or glide-reflection is the
identity permutation or interchanges two colors. Hence the coloring is
perfect.
In (3,4,6,4) the assignment of four colors at some vertex determines all
other colors. The reason for this is that the three squares around a
triangle must have three different colors. This determines the colors of
the hexagons at the vertices of the triangle, etc. The eventual result is
that all triangles are the same color, yellow in Figure 3. That this
coloring is perfect can be verified visually (with some patience!).
Similarly, in (3,6,3,6) the three hexagons around a triangle must have
three different colors, which in turn determines the colors of the
triangles at the vertices of this triangle, etc. The result is shown in
Figure 4, which can be visually verified to be a perfect coloring. Note,
however, that in contrast to Figure 3 all colors are congruent; in fact any
two of them can be interchanged by a translation.
(iii) We propose to show that when the colors
a, b, c, d, e are assigned
to the two triangles, square, triangle, square around one vertex (in that
cyclic order) then there are exactly two ways that assignment can be
completed to yield a chirally perfect precise coloring of the entire tessellation.
For this purpose denote the midpoint of the edge between triangles a and b
by P; denote the center of square c by Q. Denote by S the square having an
edge in common with triangle b and a vertex in common with square c. Then
S must be colored d or e.
First case: S is colored e. Then a half-turn about P, rot P, fixes color
e and interchanges a and b. Hence rot P is the permutation (ab) or
(ab)(cd). If rot P = (ab) then the quarter-turn around Q, rot Q (which has
period 2 or 4 and fixes colors c and e) must be (bd). Using rot P and rot
Q repeatedly, the "precise" condition yields a unique precise coloring.
However, the resulting coloring is not consistent with translations, and
hence is not chirally perfect. On the other hand, if rot P = (ab)(cd) then
again rot Q = (bd). Then rot P, rot Q and translations determine a unique
precize coloring, which is shown in Figure 5. It is chirally perfect, but not
perfect.
Second case: S is colored d. Then rot P = (ab)(de). It follows that rot Q
(taken to be in the direction that takes b to d) is (abde). Then rot P,
rot Q and the "precise" condition determine a unique coloring, which is
chirally perfect, but not perfect.
Note that in Figure 5 there is an exceptional color, gray (color e in the
first case above, and color c in the second case), which occurs only in
squares, whereas the other four colors appear in both squares and
triangles. If Figure 5 is reflected in a line then it is
equivalent to the coloring obtained in the second case above. The gray
squares are the ones colored c, and the other colors are a permutation of
the colors of the first case.
(iv) First, consider the case where not all hexagons are the same color.
Let T be a triangle with no edge in common with a hexagon. Suppose this
triangle is colored t, and the three triangles at its edges are colored
b, c, d. Since not all hexagons are the same color we can choose T so
that the three hexagons having edges in common with these three
triangles do not all have the same color. If one of these hexagons is
colored e, then the "precise" condition at the vertices of T eventually
implies that all three have color e, contradicting our original
assumption. Then, given that none of these
hexagons is colored e (and none is t, since each shares a vertex with
T), the "precise" condition determines each of their colors. With this
begining (and resolving occasional apparent dichotomies) a unique
precise coloring, shown in Figure 6, is obtained. Remarkably, the local
"precise" condition has been enough (as it was in the four simpler cases
treated in (ii)) to guarantee that this coloring is chirally perfect.
Next, suppose that all hexagons are the same color, say e. Assign
colors a, b, c, d to the four triangles at a vertex, E, of one of these
hexagons, in cyclic order (so that a and d are the colors of the
triangles sharing an edge with E). Let rot E be the permutation of
colors induced by rotation by a one-sixth turn around the center of E
(in the direction from color a to color d). Let rot P be the rotation
about the midpoint, P, of the edge between triangles colored a and b.
Then the permutation of colors induced by rot P is (ab)(cd) or (ab).
If rot P is (ab)(cd) then the only apparent possibilities for rot E
are (ad), (adb), or (adc). Filling in the colors of triangles around E
shows that the first two lead to contradictions. The case of rot E =
(adc) yields Figure 7, which is chirally perfect.
If rot P is (ab) then there are the same three possibilities for
rot E. In this case, only rot E = (ad) succeeds. The result is shown in
Figure 8, which is chirally perfect.
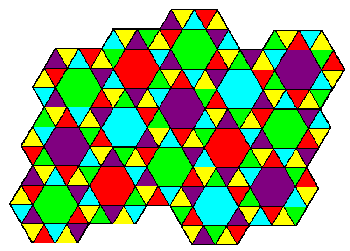
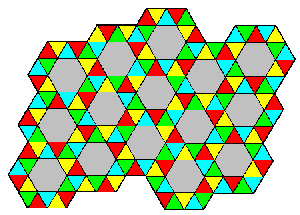
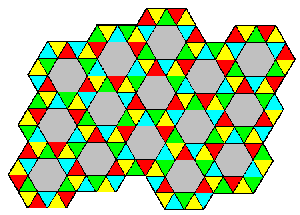
Figures 6-8
(v) The tessellation (3,3,3,4,4) is naturally viewed as horizontal rows
of squares separated by rows of triangles. If the three triangles and
two squares at a vertex on the upper edge of a row of squares are
colored a, b, c, d, e in
that cyclic order (triangles a, b, c; squares
d, e) then triangle next to c must be colored either a or e.
First case: The triangle next to c is colored a. Then the square (in
the row above) sharing an edge with this triangle must be colored d or
e. These two possibilities turn out to lead to colorings which reflect
into each other; hence we assume this square is colored d. Then the
permutation induced by translation V (up and to the right) fixes d and
e. Consistency of the coloring with translations only requires that V
permute a, b, c arbitrarily. However, for consistency with half-turns
about centers of squares only the three even permutations of a, b, c are
permitted. These three even permutations yield Figures 9, 10 and (the
reflection of) Figure 11. (This reflection of Figure 11 is the one
obtained when V is the identity permutation of colors.)
Second case: The triangle next to c is colored e. Then the colors of
three of the squares in the next higher row are immediately determined.
From this, and the "precise" condition, the permutation of colors
induced by V is (edacb). It is easy to see that the entire coloring is
thereby determined. The result is shown as (the reflection of) Figure
12.
It is easily seen, since the two colors in the rows of squares
never occur in the rows of triangles in Figures 9, 10, 11, that
uncountably many precise (but not chirally perfect) colorings of
(3,3,3,4,4) result by arbitrarily sliding rows of squares to the right
or left.
This completes the enumeration of all precise perfect (or chirally
perfect) colorings of the Archimedean tessellations.
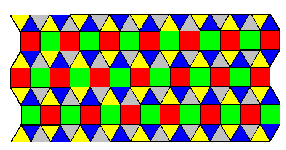
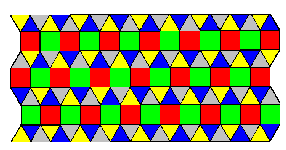
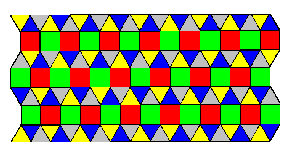
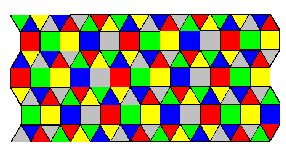
Figures 9-12
Acknowlegments: The author is indebted to John Rigby for the initial ideas as well as for
correcting an omission in an earlier version, and to Bob Wilson for
assistance with the computerization.
Received: 27 November 1998