But symmetry need not be limited to geometry and algebra. Let us consider the notion
of Magic Squares.
There are many problems associated with magic squares. E.g.,
What must be the sum of each row in a 10×10
normal magic square?
Students seem to love problems with magic squares, but constructing
the square itself, even a normal magic square, is not easy. There are two
main classes of normal magic squares of order n; those for
which n is odd and those in which n is even. And for those
which are of even order, there is a further classification; those for which
4 is a divisor of n, and those for which
it is not. For each of these there is
a different algorithm to construct them. Because of space limitations we
will only look at magic squares of odd order. (A comprehensive discussion
of the underlying theory, construction and generalizations of magic squares
is given in Ball (1949).)
The following algorithm can be extended to all magic squares of odd
order; we exemplify it in Figure 4 for the 3×3 case. Start with 1
in the top middle cell. Now move along the diagonal, always moving upward
and to the right. If in so moving, we find ourselves outside of the square's
frame at the top, we continue filling in the cells of the square at the
bottom of that column (Fig 4a). If we find ourselves outside the frame
on the right, we move to the first cell on the left of that row (Fig.4b).
If a cell is blocked within the frame itself because we have already filled
it in, we drop to the cell immediately under the one from which we came,
fill it in (Fig.4c) and continue filling in the square moving upward and
to the right.
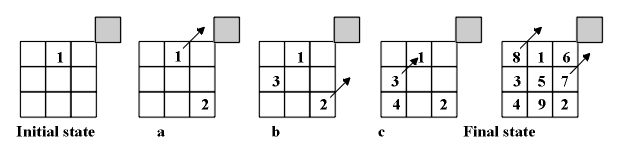
Figure 4
There are several ways to see that the square is really magic. One
way is to actually check the sums in each row, column and diagonal. Another
is a little easier; e.g., to check to see if a 5×5 square is indeed
magic, write each number in each cell in base 5.
Now from the number in each cell subtract one from its base 5 representation.
What remains is all combinations of two digit numbers in base five.
It can be seen that each row and column and one of the diagonals
are some permutation of the same digits. In other words, one need not do the
actual computations, but simply check to make sure that all digits are there.
Students love to play with magic squares, but they are often unable
to construct ones which are not normal. Here is where symmetry can enter
because all magic squares of order 3 are
of a particular form as shown in Figure 5.
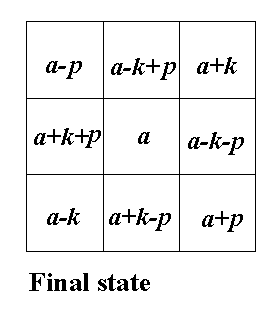
Figure 5
Students are often amazed at how simple this is for them
and they often try to generalize the method of building symmetry
along the diagonals of higher ordered squares. This exercise opens up many
doors for discussion, building in symmetry to effect a solution and degrees
of freedom are just two avenues for deeper work.
Symmetry in cubic polynomials:
There are two ways to prove that every cubic polynomial is symmetric
about its point of inflection. A cubic polynomial is one of the form f(x)
= ax3 + bx2 + cx + d and
its general graph is listed in Figure 6.
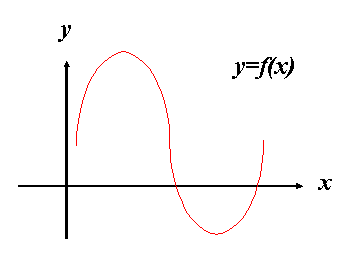
Figure 6
Its point of inflection is at
(-b/3a, f(-b/3a)),
So, using its graph to guide us we wish to show that:
f((-b/3a)-x)-f(-b/3a)
= f(-b/3a)-f((-b/3a)+x)
The algebra is not easy but straightforward.
Another way to do the problem is to play on its symmetry from the start.
First we look at the graphs of y = x3 and y
= (x-1)x(x+1). Each of these graphs has its point
of inflection on the y-axis, and the students easily prove that
the graphs are symmetric with respect to their point of inflection. We
then talk about the effect of adding a constant to the above equations,
y
= x3+k, y = (x-1)x(x+1)
+ k. The students immediately realize that the effect of adding
a constant to equations of this type simply pushes the graph up or down
the y-axis; their points of inflection remain on the y-axis
and thus the symmetry remains intact. The students thus realize that
an equation of the form y = x3 + Bx + C
has
a point of infection on the y-axis and that its graph is symmetric
about it.
We then return to the given equation and ask if there is some way to
transform it into one that will result in a cubic of
the form y = z3 + Bz + C. The transformation
x
= z - b/(3a) will move
the graph horizontally so that its point of inflection is on the
y-axis. In effect this gives
another proof that cubic equations are symmetric about their point of
inflection.
Summary
In this paper we have tried to show that symmetry is a concept which
can be exploited and used as a red thread connecting different branches
and skills in school mathematics. But the main message we have tried to
argue is that symmetry must be taught. It is too useful and important of
a topic to let it develop casually, if at all, as one passes through the
school curriculum.
Acknowledgment
We would like to thank Slavik Jablan for the
wonderful animation of the static diagrams we submitted to him, and for
the suggestions he made for improving the original draft of this
paper as well as for the encouragement he gave us along the way.