|
In the history, the European musical theory and aesthetics constituted by an empirical-rational method the system of musical rules: the laws for the construction of musical works, based on seven-tone tonality. The major - minor tonal system with a tonic as the tonal center dominated in the whole European musical tradition for the centuries. From the basic statement that the laws of mathematics and proportions (arithmetical, geometrical and harmonical) could describe the nature, Pythagoreans derived the theory of musical harmonies, identifying it with the harmony of the well-organized universe. Beginning from the tetrakis – 1, 2, 3, 4 – the ordered sequence of small natural numbers, and forming their proportions 1:2, 2:3, 3:4, the three basic proportional vibrations - octave (1:2), perfect fifth (2:3) and perfect fourth (3:4), and the natural overtone series are derived. Pythagoras (or the Pythagoreans) made two important statements with regard to them, one an aesthetic claim, the other a mathematical observation. The aesthetic claim was that they believed that each of the planets emitted a tone, and that the universe thus resonates with a "music of the spheres" of which the natural overtone series on our earth is only an image. The mathematical observation regarded the circle that can be built from the interval represented in the second proportional vibration 2:3 (the perfect fifth), in relation to the sequence built from the first, 1:2 (the octave). In solving the problem of the Pythagorean comma (the difference between the tone obtained as a result of stacking twelve consecutive perfect fifths from that reached in seven octaves), as the result of tempering (the tuning based on perfect fifths and octaves) it was obtained the chromatic scale with twelve equal semitones. (Well-tempered tuning was devised by Werckmeister, a contemporary of J.S. Bach, hence the "Well-tempered Clavier"). The tones of that scale may be simply denoted as 0,1,...,11 (mod 12), where the enharmonic tones are treated as the same, and where the unit is a semitone. In fact, the result was a symmetrization: the division of octave in twelve equal semitone intervals. During the history, from all modes two of them are distinguished: the major (Ionian) and minor (Aeolian). In the sense of their meaning and emotional-symbolical role they are a well-known example of antisymmetry . According to the notation introduced, C major will be represented by the sequence 0,2,4,5,7,9,11, D major by 2,4,6,7,9,11,13, C minor by 0,2,3,5,7,8,10, etc., where all that sequences are periodic mod 12. To every major corresponds the same sequence of intervals (measured from the first tone): 0,2,4,5,7,9,11, and to every minor the sequence 0,2,3,5,7,8,10. The interval i between any two tones will be the number of semitones between them (i.e. the difference of the numbers corresponding to that tones), so to the octave corresponds the interval 12, to the perfect fifth the interval 7, to the perfect fourth the interval 5, etc., where all tones and intervals could be reduced mod 12 (so-called vertical reduction). For a reduced interval i, its complement is i'=12-i. Except the mentioned (global) antisymmetry, in every tonality we could discover the basic (local) antisymmetry: the relationship between the complementary intervals (e.g. third – sixth, forth - fifth...). The only interval, equal to its complement is the tritone interval (i=6), the ambiguous interval having a double meaning (unperfect forth (i=6=5+1) or unperfect fifth (i=6=7-1)), the main dissonance, center of instability in every tonality. If we identify the complementary intervals (i.e. if we reduce them to the minimal interval between two tones by taking min(i,i') reduced mod 12), for every two tonalities we could consider the number of their joint tones in an octave, called the coefficient of similarity. In the following table (Fig. 1), in the case where the both of tonalities are natural majors or natural minors, this coefficient is denoted by k, and i is the interval between the first tones of the considered tonalities. For example, for C major (0,2,4,5,7,9,11), and D major (2,4,6,7,9,11,13), the interval between their first tones is i=2, and because in one octave they have five joint tones (2,4,7,9,11), their coefficient of similarity is k=5; for c minor and f minor we have i=5 and k=6, etc. For two tonalities, where the first of them is a major, and the other a minor, the coefficient of similarity is denoted by K; if the first tonality is a minor, and the other a major, it is denoted by K', and i is, as before, the interval between their first tones. For example, for C major and d minor, we have i=2 and K=6; for d minor and F major i=3 and K'=7, etc.
This way, we could notice the first (anti)symmetry property: the coefficients of
similarity for the tonalities of the same type
(major -
major or
minor -
minor) are mirror symmetrical,
and the coefficients of similarity of opposite tonalities
(major - minor)
are point-symmetrical. In the both cases,
the symmetry element (the mirror axis or the center of
symmetry) coincides with the point 6, this means, with the
tritone
interval (i = 6) (Fig. 1).
Continuing with this approach, we may prove the remarkable
fact: the tonal system
major -
minor is completely invariant
with regard to the
complementarity of intervals.
First, we could try to explain, by using only the symmetry arguments, the
reasons for the priority of
major (Ionian) -
minor (Aeolian) modes in the
complete system of modes, and to show why exactly
those two modes (Ionian and Aeolian) are distinguished (by the empirical
"natural selection") in the history of European music.
The basis of all modes is the periodic tone sequence
...0,2,4,5,7,9,11... with the period 12. All particular
modes are derived from it by different choices
of the beginning point. For example, if we start from 0
and reduce all the intervals to their minimal intervals
(i.e. if we identify the complementary intervals with
their minimum), the following table of the interval
structure for all possible
modes is obtained:
0 2 4 5 5 3 1 that could be, according 0 2 4 5 5 3 1
If we denote the intervals 6, 5,
4, 3, 2, 1
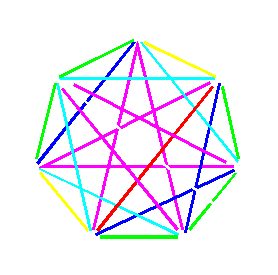
by the corresponding colored lines, as the result we obtain the following circle diagram (Fig. 2).
From that diagram, we can notice two important properties: (1) the singularity
of the interval i=6; (2) the
mirror-symmetry of the diagram. The mirror axis contains the point 2 and passess
between the points 7 and 9. We could observe here the
tritone triangle
with the vertices 2,5,11. Because it represents the center of instability, its vertices
are not acceptable for the first tone of any tonality. Among the remaining points
we have two pairs of mirror-symmetrical (this means, equivalent) points: 0,4 and 9,7.
This means, that we have only two possible nonequivalent beginning points: 0 and 9.
Taking the first, we obtain the sequence of the intervals 0,2,4,5,7,9,11
corresponding to all major
tonalities (Ionian mode), and from the other
results the sequence 0,2,3,5,7,8,10, corresponding to all
minor tonalities (Aeolian mode).
Because the tritone triangle is the center of instability in every tonality,
for any triad (or chord) we may define its coefficient of stability s as
s=3-t (or s=4-t for a four-tone chord),
where t is the number of
the joint tones of that triad (or chord) with the tritone triangle.
The already noticed mirror-symmetry remains preserved
in all the harmony levels: in the
(anti)symmetrical distribution of
major and
minor triads and chords, in the position of
the main and other harmony functions (T,
S,
D,
s,
d),
in the distribution of the coefficients of stability, etc.
Different symmetries, resulting from
the basic symmetrical organization of the tonal system
occur in the case of all triads and chords, and together with
their individual symmetries represent the standardized
patterns of tonal music.
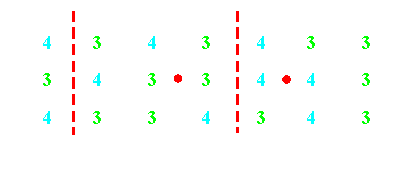
Figure 3 shows all the seven possible four-tone chords (given by the intervals)
and their symmetries. The mirror-axes are denoted by the white lines,
antisymmetry axes by the red broken lines, and the centers of
antisymmetry by the red dots.
This way, after the mutual identification of
complementary intervals (e.g. third –
sixth,
forth -
fifth...),
(i.e. by reducing all the
intervals between two tones to the minimal ones),
we succeeded to discover the basic symmetry of the
major - minor tonal system:
its complete invariance with regard to the
complementarity of
intervals. As the result, all the important parameters
of the tonal system (e.g. number of joint tones for two
tonalities, the chord structure of every tonal system,
etc.) are symmetrical with regard to the
tritone
interval i=6.
From this basic symmetries resulted a large
number of symmetries in the complete harmony level
of the tonal music. So, in the beginning it was
the ORDER.
|