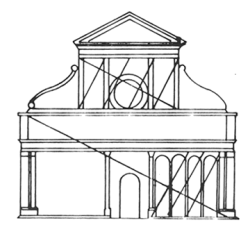
Figure 2. Santa Maria Novella |
|
During the Renaissance a simple geometric principle was used to create duplicates of a given proportion at a reduced scale as illustrated in Figure 2 for Santa Maria Novella. |

Figure 2. Santa Maria Novella |
|
Given a rectangle of arbitrary proportions 1:x as shown in Figure 3a, draw the diagonal and then another diagonal intersecting the first at right angles. This divides the original unit (U) into a smaller unit and a leftover rectangle referred to as a gnomon (G), i.e., U = U + G as shown in Figure 3b. Of course this can be repeated to obtain a dissection of U into an arbitrary number of "whirling" gnomons and one leftover unit (see Figure 3c). The vertices of the gnomons lie on a logarithmic spiral as shown in Figure 3c. |
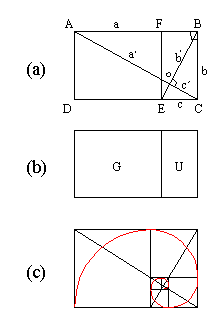
Figure 3. a) The law of repetition of ratios; b) a unit divided into a unit (U) and a gnomon (G); c) vertex points form a logarithmic spiral. |
|
This concept has been popularized by the twentieth century designer Jay Hambridge who referred to it as dynamic symmetry [Hambridge 1929], [Edwards 1968]. In Figure 4a the law of repetition of ratios is applied to a golden rectangle of proportions 1 : f to obtain a gnomon equal to a square (S), i.e., G = S. In Figure 4b dynamic symmetry is applied to a rectangle of proportion 1:q, which we refer to us as a Roman rectangle, to obtain a gnomon of a double square, i.e., G = S + S. In Figure 4c, for a rectangle of proportions 1 : y, we obtain G = S + S + U. For a rectangle of proportions 1: Ö 2, G = U, i.e. , if the root 2 rectangle is divided in half, two root 2 rectangles are created (see Figure 4d). For a rectangle of proportions 1: Ö 3, G = 2/3 U, i.e., the unit is the 1/3 part of the original rectangle (Figure 4e). |
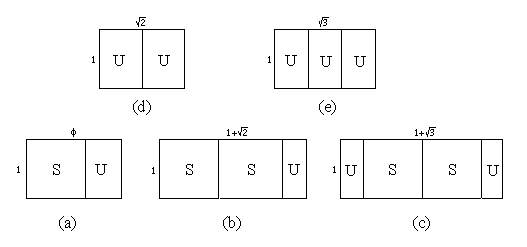
Figure 4. Law of repetition of ratios where the unit is a) a golden rectangle; b)a Roman rectangle; c) a 1 + Ö 3 rectangle; d) a root 2 rectangle; e) a root 3 rectangle. |