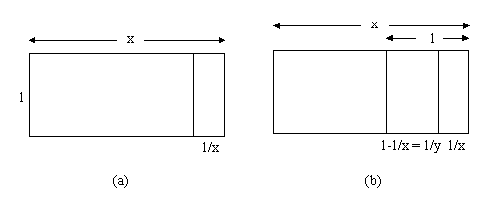
Consider a rectangle of proportions 1: x subdivided according to the law of repetition of ratios into a unit of the same ratio and a gnomon (see Figure 6a). In Figure 6b a square placed into this rectangle produces a pair of proportions 1/x and 1-1/x = (x-1)/x = 1/y where 1/x + 1/y = 1. If x and y are irrational numbers then we can apply Beatty's Theorem.

Theorem (Beatty's):

If x and y are irrational numbers such that 1/x + 1/y = 1 (Beatty pairs), then the set {[nx], [ny]} for n = 1,2,3,..., where [ ] denotes "the integer part of", equals the set of natural numbers with no repeats.

The following Beatty pairs correspond to the golden mean, root 2, and root 3 systems of proportion, respectively: 1) x = f, y = f²; 2) x = Ö2, y = qÖ 2; and 3) x = Ö3, y = a Ö3. Table 1 illustrates Beatty's Theorem for the Ö3 system.

If the numbers in column 2 are assigned a 1 while the numbers in column 3 are assigned a 0, the numbers in Table 1 are listed in order as

This sequence is known in the theory of dynamical systems as the symbolic dynamics. Notice that it contains all the information concerning the approximating sequence to Ö 3 given by sequence 8a. For example 1/2 of the first two numbers in sequence 12a are 1's, 3/5 of the first five numbers are 1's, 11/19 of the first 19 numbers are 1's, etc. In a similar manner the symbolic dynamics for the f system and the Ö 2 system are:

f:            1 0 1 1 0 1 0 1 1 0 1 1 0 1 0 1 1 ...          (12b)
Ö2:          1 1 0 1 1 0 1 1 1 0 1 1 0 1 1 1 0 ...          (12c)

These also replicate their approximating sequence 3 and 5.

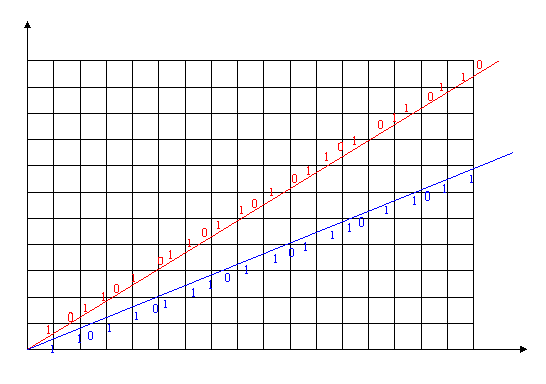
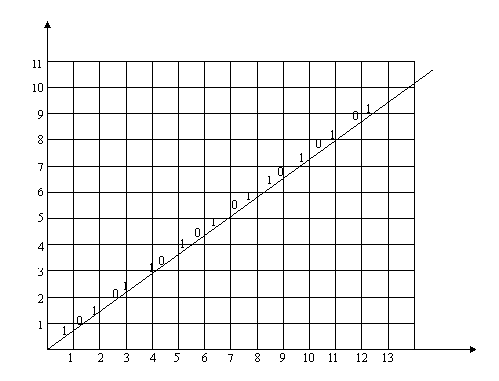
The symbolic dynamics can also be generated by drawing a line with slope x/y on a coordinate system with vertical and horizontal lines drawn at integer values of the coordinates. Where this line cuts a vertical coordinate line assign a 1; where it crosses a horizontal coordinate line assign a 0. The symbolic dynamics for the f, Ö2, and Ö3 systems is illustrated in this manner in Figure 7. The ratio, 1/x, can be thought of as the probability of getting a 0 in the above sequence while 1/y is the probability of getting a 1, in which case the slope of the line represents the odds of getting a 0.

Figure.7a. Square lattice and straight line with slope x/y = 1/f generates the approximating sequence (10110...) to f. The lower straight line has slope x/y = 1/q and generates another self-similar approximating binary sequence to Ö2.

Figure 7b. Square lattice and straight line with slope x/y = 1/a generates the Ö3 approximating sequence.