Introduction|
Special Case of Architecture | Overview of Symmetry Types | Multiple
Symmetries in Architecture | Symmetry in Architectural
Space |
Conclusions | Acknowledgements
| Notes | Related
Links
Symmetry in Architecture
Kim Williams, Architect
Via Mazzini 7
50054 Fucecchio (Firenze) Italy
e-mail: k.williams@leonet.it
Introduction
What does the seventeenth-century Rundetarn
(Round Tower) of Copenhagen have in common with the thirteenth-century
Leaning Tower of Pisa? Or Houston's Astrodome, the first indoor
baseball stadium built in the United States, with the vast dome
of the Pantheon in Rome? Or a Chinese pagoda  (fig.
1) with the Sydney Opera house (fig. 2)
(fig.
1) with the Sydney Opera house (fig. 2) ?
A first response might be "shape" but a more accurate
answer would be "symmetry". Each of these strange couples
of buildings share a different kind of symmetry that links them,
in spite of their temporal and cultural differences. As Magdolna
and István Hargittai have noted, symmetry, in architecture
as in other arts, is "a unifying concept".[1]
?
A first response might be "shape" but a more accurate
answer would be "symmetry". Each of these strange couples
of buildings share a different kind of symmetry that links them,
in spite of their temporal and cultural differences. As Magdolna
and István Hargittai have noted, symmetry, in architecture
as in other arts, is "a unifying concept".[1]
Architecture, as any compositional art, makes extensive use
of symmetry. Across all cultures and in all time periods, architectural
compositions are symmetrically arranged. There are so many kinds
of symmetry, so many kinds of architecture, and so many ways of
viewing architecture, that the argument threatens to become so
generalized that it loses all meaning. The general exposition
of symmetry types found in architecture has been admirably presented
in recent work.[2] While
I wish to review symmetry types in architecture briefly in order
to provide as wide an overview as possible within the limits of
this paper, my ultimate object is to explore why an architect
might choose a given symmetry type, and thus to provide insight
into the design process from the point of view of symmetry.
The special case
of architecture
Architecture differs fundamentally from
other arts because of its spatiality. Identifying a type of symmetry
in a two-dimensional composition is relatively straightforward;
the identification of symmetry types in a three-dimensional object
such as a sculpture is somewhat more complicated because our perception
of the object changes as we move around it. In the case of architecture,
we not only move around it, but we move through it as well. This
means that architecture provides us with a special opportunity
to experience symmetry as well as to see it. This is possible
because architecture consists of two distinct components: solid
and void. Architecture is most frequently characterized by the
nature of its elements: we recognize a Greek temple by its portico
and pediments; a Gothic cathedral is characterized by its pointed
arches and flying buttresses. These are the elements that make
up the solid component of architecture, and it is likely that
it is with this solid component the lay person has the most experience.
Naturally in the composition of these elements that one would
expect to find various kinds of symmetry relations, and this,
the symmetry that we see, is what I will be examining in the first
part of this paper.
On the other hand, all these solid elements constitute an envelope
around what we experience when we move through a building, that
is, the void, or architectural space. In a very real way, the
true work of the architect is to shape the void, which becomes
the theater of the actions that take place in the building. This
architectural space is most likely characterized by symmetry as
well, though it is perhaps less familiar, and it is a symmetry
which we experience. This is what I will examine in the second
part of this paper.
An Overview of
Symmetry types in Architecture
Symmetry types are divided into two
categories: point groups and space groups. Point groups are characterized
by their relationship to at least one important reference point;
space groups lack such a specific reference point. Both point
groups and space groups are found in architecture.
Bilateral symmetry is
by far the most common form of symmetry in architecture, and is
found in all cultures and in all epochs. In bilateral symmetry,
the halves of a composition mirror each other. It is found in
the facade of the Pantheon in Rome; some 1700 years later on a
continent undreamed of when the Pantheon was built, we find the
same symmetry in the mission-style architecture of the Alamo in
San Antonio, Texas. Bilateral symmetry is present also not only
on the scale of a single building, but on an urban scale. An example
of this is found in the design of the PraHo do Comercio in Lisbon,
Portugal, where three urban elements (a major public square, a
monumental gate and the wide commercial street beyond the gate)
are symmetrical with respect to a long horizontal axis that governs
our visual perspective.
The popular of bilateral symmetry is probably an expression of
our experience of nature, and in particular with our experience
of our own bodies. As many cultures believe that God created man
in His own image, architecture has in turn probably been created
in the image of man. Not all bilateral symmetry is of equal value
in architecture, however. Two schemes for facades are shown in
fig. 3. 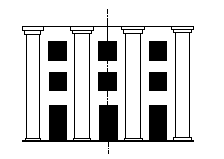 In one, there are
an unequal number of bays; in the other, there are an equal number
of bays. The first is an example of "orthodox" bilateral
symmetry, where the facade is divided into two equal halves; but
in the second, the axis of symmetry that divides the facade into
two equal and independent halves creates a dualism. If it is true,
as Dagobert Frey maintains, that bilateral symmetry represents
"rest and binding"[3], then dualism represents divisibility.
In one, there are
an unequal number of bays; in the other, there are an equal number
of bays. The first is an example of "orthodox" bilateral
symmetry, where the facade is divided into two equal halves; but
in the second, the axis of symmetry that divides the facade into
two equal and independent halves creates a dualism. If it is true,
as Dagobert Frey maintains, that bilateral symmetry represents
"rest and binding"[3], then dualism represents divisibility.  Traditionally, dualism in architecture
has been considered something to be avoided. The temples of ancient
Greece, for example, always had an even number of columns so that
there was never a column on the central axis of the facade. The
avoidance of the dual by classical architects probably stems from
the ambiguity frequently attributed to the number 2, regarding
with suspicion from the time of Pythagoras. The number 2 was considered
untrustworthy (a female number) because it could be divided into
halves, in contrast to the number 3 (a male number) which was
not divisible into two parts. Even in modern architectural theory,
dualism in architecture is considered a "classical and elementary
blunder" and identified with the "amorphous or ambiguous".[4] These reservations
not withstanding, dualism does exist in architecture. The fourteenth-century
Oratory of Orsanmichele in Florence is an example (fig.4).
Traditionally, dualism in architecture
has been considered something to be avoided. The temples of ancient
Greece, for example, always had an even number of columns so that
there was never a column on the central axis of the facade. The
avoidance of the dual by classical architects probably stems from
the ambiguity frequently attributed to the number 2, regarding
with suspicion from the time of Pythagoras. The number 2 was considered
untrustworthy (a female number) because it could be divided into
halves, in contrast to the number 3 (a male number) which was
not divisible into two parts. Even in modern architectural theory,
dualism in architecture is considered a "classical and elementary
blunder" and identified with the "amorphous or ambiguous".[4] These reservations
not withstanding, dualism does exist in architecture. The fourteenth-century
Oratory of Orsanmichele in Florence is an example (fig.4). It has a dual function: an oratory
on the ground floor and a granary above. It has an unusual two-aisled
plan. It has two altars. The difficulty of the dual on the level
of architectural experience is best exemplified by the problem
of the two altars. Where does one stand in the church? One is
forced to make a decision whether to stand in front of one altar
or the other. It is comparable to a house with two front doors.
Where is the entrance? Usually this kind of decision is made for
the spectator by the architect, who places one altar in a central
position, or one prominent front door on the facade of a house.
Thus, dualism in architecture presents a kind of a challenge to
both the spectator and the architect.
It has a dual function: an oratory
on the ground floor and a granary above. It has an unusual two-aisled
plan. It has two altars. The difficulty of the dual on the level
of architectural experience is best exemplified by the problem
of the two altars. Where does one stand in the church? One is
forced to make a decision whether to stand in front of one altar
or the other. It is comparable to a house with two front doors.
Where is the entrance? Usually this kind of decision is made for
the spectator by the architect, who places one altar in a central
position, or one prominent front door on the facade of a house.
Thus, dualism in architecture presents a kind of a challenge to
both the spectator and the architect.
Rotation and reflection
provide a sense of movement and rhythm in architectural elements
and an emphasis on the central point of the architectural space.
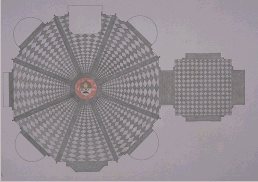 The Sacristy of the
basilica of S. Spirito in Florence, designed by Giuliano da San
Gallo in the last years of the fifteenth century, is octagonal
in plan and both the architecture and the distinctive pavement
design exhibit rotational and reflection (fig. 5). Domes, whether
hemispherical such as that of the Pantheon or octagonal such as
the great cupola of the Cathedral of Florence designed by Filippo
Brunelleschi, also exhibit both rotation and reflection.
The Sacristy of the
basilica of S. Spirito in Florence, designed by Giuliano da San
Gallo in the last years of the fifteenth century, is octagonal
in plan and both the architecture and the distinctive pavement
design exhibit rotational and reflection (fig. 5). Domes, whether
hemispherical such as that of the Pantheon or octagonal such as
the great cupola of the Cathedral of Florence designed by Filippo
Brunelleschi, also exhibit both rotation and reflection.
Cylindrical symmetry is
that found in towers and columns Verticality in towers represents
a defiance of gravity. Rare examples of spherical symmetry may
also be found in architecture, though the sphere is a difficult
form for the architect because human beings move about on a horizontal
plane. The project for a cenotaph for Isaac Newton, designed by
Etienne-Louis Boulée in 1784, demonstrates spherical symmetry.
Chiral symmetry is perhaps
less well-known than other types of symmetry but frequently effectively
used in architecture. Chiral symmetry is found in two objects
which are each other's mirror image and which cannot be superimposed,
such as our hands.  The
two opposing colonnades designed by Gianlorenzo Bernini that surround
the elliptical piazza in front of St. Peter's in Rome exhibit
chiral symmetry (fig.6). In Budapest, the two Klotid Palaces that
tower above Felszabadul<s Square, each with asymmetrically
placed towers and facade embellishments, are examples of chiral
symmetry. A very subtle form of chiral symmetry is presented by
the two leaning towers of the newly-completed Puerta de Europa
in Madrid, designed by architect John Burgee in collaboration
with Philip Johnson. Chiral symmetry in architecture is another
way to place visual emphasis on the central element of a composition.
In the case of the Puerta de Europa, for example, the two inclined
towers emphasize the broad boulevard that passes between them,
aptly forming a "gateway to Europe".
The
two opposing colonnades designed by Gianlorenzo Bernini that surround
the elliptical piazza in front of St. Peter's in Rome exhibit
chiral symmetry (fig.6). In Budapest, the two Klotid Palaces that
tower above Felszabadul<s Square, each with asymmetrically
placed towers and facade embellishments, are examples of chiral
symmetry. A very subtle form of chiral symmetry is presented by
the two leaning towers of the newly-completed Puerta de Europa
in Madrid, designed by architect John Burgee in collaboration
with Philip Johnson. Chiral symmetry in architecture is another
way to place visual emphasis on the central element of a composition.
In the case of the Puerta de Europa, for example, the two inclined
towers emphasize the broad boulevard that passes between them,
aptly forming a "gateway to Europe".
Similarity symmetry is
currently receiving a great deal of attention and is best known
for its identification with fractals. Similarity symmetry is found
where repeated elements change in scale but retain a similar shape,
such as in the layered roofs on a pagoda (see fig. 1 above), the
forms of which diminish in size but retain their form as they
get closer to the top of the building. Another example of similarity
symmetry is found in the nestled shells of the Sydney Opera House,
designed by Joern Utzon in 1959 (see fig. 2 above). The shells
are all segments of a sphere, thus similar in shape while differing
in size and inclination. Another example of similarity symmetry
is found in the Castel del Monte in Apulia in Italy, built by
Friedrich II at the end of the first millennium. The basic form
of the octagonal outer walls of the fort is repeated at a smaller
scale in the interior courtyard, and again in the smaller towers
which are added to each apex of the main octagon.[5]
Similarity symmetry is also often used
where it is least obvious, as in the relationships between room
sizes. Frank Lloyd Wright used a kind of similarity symmetry in
his design for the Palmer House in Ann Arbor, Michigan, in 1950-51.[6] In this case,
Wright chose an equilateral triangle as a planning module, repeated
at a number of levels and sizes to organize the design of the
house. Similarity symmetry, whether visually apparent or not,
results in a high degree of order within an architectural design,
and lends unity to a composition.
Spiral or helical
symmetry may be thought of as a special kind of similarity
symmetry. Helixes and spirals in architecture often represent
continuity. In spiral staircases, the unbroken form expresses
the continuity of space from level to level throughout the building.
In the fantastic twisted spires of Copenhagen or of Borromini's
S. Ivo alla Sapienza in Rome, the theme of continuity is expressed
by the unbroken upward progression of the form. Frank Lloyd Wright
used the helix in his 1946 design of the Guggenheim Museum of
New York. In this case, the exterior of the building reflects
the form of the giant helical ramp on the interior. The gallery
spaces are arranged along one side of the ramp. The museum visitor
takes the elevator to the top floor of the space, then spirals
his way down the ramp to the bottom, admiring the art on display
along the way. Criticism of the building focused on the fact that
the downward spiral forced the visitors to hurry through the museum,
unconsciously rushed by the pull of gravity. Legend has it that
Wright, who placed greater value on architecture than on art,
deliberately designed the building in order to get the visitor
out as quickly as possible! In reality, however, the helical ramp
once again expresses spatial continuity.
Translational symmetry
falls in the category of space group symmetry, and is, after bilateral
symmetry, the most common kind of symmetry found in architecture.
Translation of elements in one direction is found in solemn rows
of soldier-like columns, or in the springing succession of arches
in an aqueduct. Translation of elements in two directions is present
in the wallpaper-like patterns of the curtainwall facades of many
modern buildings. Translation may also involve the repetition
of entire pieces of buildings, especially in our own century,
and may be one reason by modern architecture is so often referred
to as boring or monotonous. Translational symmetry seems to carry
with it an emphasis on a superlative quality in architecture:
the longest, the broadest, the tallest.
This concludes my survey of types of symmetry found in arrangements
of architectural elements. For the architect, the knowledge of
symmetry types is a powerful tool, for it provides him not with
a means for precisely describing a building, but with a range
of expressive possibilities. We will learn more about the expressive
possibilities of symmetry when we look at the use of symmetry
in architectural space. However, before turning to this, I should
emphasize another aspect of symmetry in architecture that makes
it a special case in the study of symmetry.
Multiple Symmetries
in Architecture
In choosing the examples of various
symmetry types for the previous section of this paper, I purposely
focused on one aspect or part of a building that exhibits a single
kind of symmetry. However, in most buildings we find more than
one kind of symmetry. For example, in the Chinese pagoda, we can
see at the same time both the cylindrical symmetry inherent in
the building's organization about the vertical axis, and the similarity
symmetry of the diminishing sizes of the layered roofs. A colonnaded
temple facade may demonstrate bilateral symmetry, but it also
demonstrates translation. These are examples of multiple symmetries
that can be observed without requiring us to change our viewpoint
of the building. We also perceive multiple symmetries when we
change our position relative to the building, as for example,
when we move from outside to inside. Domes are a very good example
of this. From the outside, domes appear to be organized about
a vertical axis (as they indeed are). When viewed from the inside,
however, they appear to be organized about a central point.
Multiple symmetries also arise when a building is composed of
multiple elements, some or all of which having its own symmetry.
The symmetry type that we identify at any given moment, then,
is a result of our physical position in relation to the building.
It is important to make this point about multiple symmetries,
because most architecture of any complexity at all is designed
as a series of spaces that are meant to be experienced sequentially,
as though the architect is telling us a story. Changing symmetries
can be as important to the unfolding of the story as any of the
other devices an architect has at his service. A closer examination
of the Pantheon will illustrate the experience of an architectural
"story".
The Pantheon in Rome is an excellent example of the experience
of multiple symmetries that is common in architecture. When we
stand in the piazza in front of the Pantheon, we notice right
away the bilateral symmetry of the principle facade. Moving around
the building, we discover that the Pantheon is composed of three
easily-identified elements: the columned porch, a small intermediate
block, and the great rotunda (fig. 7).  The
three are arranged in sequence: here is the beginning of the "plot"
of the story. As we enter the Pantheon, we see that the three
elements are arranged with respect to a common horizontal axis;
it is this axis that gives rise to the bilateral symmetry. However,
once inside, the horizontal axis that we have followed to gain
entrance into the rotunda disappears. It is replaced by a vertical
axis that runs from the center of the pavement up to and through
the oculus of the dome above. Thus the dominant symmetry is no
longer bilateral. The lower zone exhibits cylindrical symmetry,
while the hemispherical dome above exhibits rotation and reflection
. The reason for the change in symmetries is that, when we enter
into the rotunda we leave behind the zone of the terrestrial,
represented by the horizontal axis, and experience the zone of
the celestial, symbolized by the vertical axis. The Pantheon is
a temple dedicated to all the gods; the universe itself is represented
in the rotunda by the form of the sphere, half of which is actually
present in the coffered cupola which crowns the space, while the
other half is only made implicit in the proportions of the space
(as mentioned before, the sphere is problematic in architecture
because human beings require a horizontal plane). The sphere contains
an infinite number of planes of reflection and rotation; its infinity
symmetry makes it an apt symbol for the cosmos.
The
three are arranged in sequence: here is the beginning of the "plot"
of the story. As we enter the Pantheon, we see that the three
elements are arranged with respect to a common horizontal axis;
it is this axis that gives rise to the bilateral symmetry. However,
once inside, the horizontal axis that we have followed to gain
entrance into the rotunda disappears. It is replaced by a vertical
axis that runs from the center of the pavement up to and through
the oculus of the dome above. Thus the dominant symmetry is no
longer bilateral. The lower zone exhibits cylindrical symmetry,
while the hemispherical dome above exhibits rotation and reflection
. The reason for the change in symmetries is that, when we enter
into the rotunda we leave behind the zone of the terrestrial,
represented by the horizontal axis, and experience the zone of
the celestial, symbolized by the vertical axis. The Pantheon is
a temple dedicated to all the gods; the universe itself is represented
in the rotunda by the form of the sphere, half of which is actually
present in the coffered cupola which crowns the space, while the
other half is only made implicit in the proportions of the space
(as mentioned before, the sphere is problematic in architecture
because human beings require a horizontal plane). The sphere contains
an infinite number of planes of reflection and rotation; its infinity
symmetry makes it an apt symbol for the cosmos.
Symmetry in Architectural
Space
Having examined how symmetry is found
in the parts of a building that we see, we may take a look at
how symmetry relates to the part of the building we don't see,
which is the void that is the architectural space. Two concepts
are fundamental in describing architectural space: center and
path. Center relates to a single important place within the larger
architectural space, such as the altar in a church. Path relates
to the spectator's movement through the space. Christian Norberg-Schulz
writes that "...centre and path are present in any church,
but their relationship differs."[7]
This relationship actually determines
how we perceive the architectural space of any given time period.
In terms of symmetry, center may be thought of as "point"
and path, as "axis." The following, very brief, examination
of some 1500 years of architectural history hopes to demonstrate
that as architectural space evolved through the centuries, so
did the dominant symmetries.
In Roman architecture, strictly observed axial symmetry gives
rise to spaces that are monumental and static, that is, generally
embodying a sense of equilibrium rather than expressing a sense
of dynamic movement.[8]
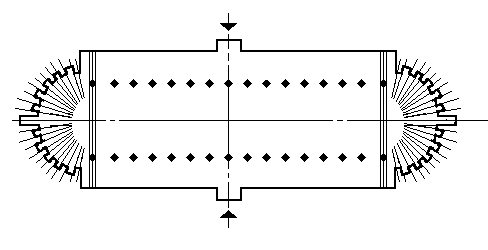
Consider the symmetry relations of the plan of a Roman basilica,
a secular building type used as a court of law (fig.8). It is
rectangular, with an apse on each end of the major axis and a
doorways on each end of the minor axis. The architectural elements
are always arranged so that like elements are always opposite:
apse to apse, column to column, doorway to doorway. Excavations
have brought to light the remains of the pavements used in basilicas;
they underline the sense of balance and equilibrium that characterize
the architecture, as frequently they are based on patterns described
by translational symmetry in two directions, rather than by any
other kind of more dynamic symmetry type such as rotation. This
same static arrangement of architectural elements is found in
the rotunda of the Pantheon, Rome. Here the plan is a circle,
with eight reflection planes and one four-fold axis of rotation
(to be precise, the symmetry is approximate because the entrance
is opposite a large round apse). Again we find oppositions: apse
to apse, aedicule (a canopied niche flanked by colonnettes) to
aedicule, niche to niche, column to column. The strict axial symmetry
establishes the sense of equilibrium within the space that is
characteristic of Roman architecture. It is interesting to note,
however, that neither the axes nor the center point is made explicit
through the pavement design of the rotunda, which is like that
of the basilica based upon translation in two directions. Thus
the symmetry was an organizing device for the architecture, but
does not determine the movement of the spectator within the space.
This is one characteristic that distinguishes Roman architecture
from that of later periods, in which we will see how axes and
centers are used to provide a specific dynamic emphasis and encourage
movement.
After the legalization of Christianity in the fourth century,
Christian architects chose to adapt the Roman basilica to their
own ecclesiastical needs. To do so, they removed the entrances
from the minor axis and placed a principal entrance on one end
of the major axis, placing the altar in the remaining apse (fig.
9).[9] 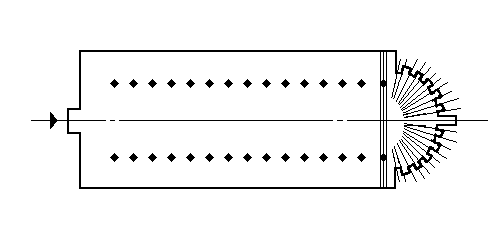
Thus the symmetry was radically altered, there remaining only
a single plane of reflection and no planes of rotation: the plan
of the Christian basilica is bilaterally symmetrical. The axis
of symmetry takes on an all-important symbolic role: it becomes
a path, symbolizing the earthly pilgrimage of the Christian making
his way towards the Kingdom of God. The pavement designs of many
of these churches make explicit the axis that governs the architecture.
Bilateral symmetry is favored over all other symmetry types during
the Early Christian, Romanesque and Gothic periods, spanning from
300 to 1300 AD, because it best expressed the Christian ideal.
It is the necessity of expressing the concept of pilgrimage, and
not only that of expressing order as suggested by Hermann Weyl,
that gave rise to the bilateral symmetry that dominated Christian
architecture up until the Renaissance.[10]
In addition to bilateral symmetry in
plan, the sense of movement along a path is underlined by the
translation of elements in a horizontal direction parallel to
the dominant longitudinal axis. It is this kind of dynamic indication
of direction that is lacking in Roman architecture.
As architectural and philosophical ideals changed in the Renaissance,
so did the type of symmetry most frequently used. Sacred architecture
was intended as a model of the cosmos created by God. To this
notion, Humanism added the concept that, because man is God's
most important creation in the cosmos, his place is in its center.
The centrally-planned building was favored as best reflecting
the perfection of the cosmos, thus rotational and reflectional
symmetries were particularly favored during this period. The center
point is usually made explicit in the pavement design: this particular
emphasis on the center point induces the spectator to place himself
there.
Pavement designs from the fifteenth, sixteenth and seventeenth
centuries use rotation, reflection and similarity symmetry to
emphasize the center. The rosette is a motif that often appears
in pavement designs of this time, as for example, in the octagonal
Sacristy of the basilica of S. Spirito in Florence (see fig.5
above). Here the rosette is formed from sections of a logarithmic
spiral. To create the curvilinear checkerboard motif, a logarithmic
segment is rotated a given number of times about the center in
one direction, forming a fan pattern, then the direction of the
segment is reversed and rotated about the center the same number
of times in the opposite direction. The resulting rosette pattern
has modules that increase in size but maintain their proportional
similarity as they move farther from the center, and is therefore
characterized by similarity symmetry as well as rotation and reflection.
Another example of paving patterns from this period may be seen
in the Cathedral of Florence, S. Maria del Fiore, in which trapezoid-shaped
modules increase in size as they move away from the pattern's
center, again demonstrating reflection, rotation and similarity
symmetry. These patterns were no doubt favored because the perspective
illusion they create is an excellent means of emphasizing the
central point of the design, and through this, the central point
of the architectural space.
Thus we see that in this arc of architectural history, the dominant
symmetry evolved from a generalized axial symmetry in the Roman
age, to bilateral symmetry in the Paleo-Christian, Romanesque
and Gothic ages, to rotational and reflectional symmetry in the
Renaissance. Our recognition of the symmetry in an architectural
space is one step towards our understanding of the architecture,
a means we are given to interpret the architectural "story"
we are experiencing.
Conclusions
At this point I draw to a close this discussion of architecture
and symmetry. I hope that the wide variety of symmetry types and
their various combinations as well as the use of symmetry to define
space has been made clear. However, the topic of symmetry in architecture
is far from exhausted. There are some further aspects of the subject
that I am now studying but about which I am not yet in a position
to draw conclusions, and for which this present paper forms a
background.
One of these aspects has to do with "broken symmetries".
The Pantheon in Rome provides one example of a symmetry break:
the cylindrical lower zone of the rotunda is characterized by
four planes of reflection and fourfold rotation, while the hemispherical
dome above is characterized by twenty-seven-fold rotation. Four
and twenty-seven have no common divisors, thus the symmetry "break."
Another example of broken symmetries is found between horizontal
tiers of the Baptistery of Pisa, which are alternately based on
rotations of twelve and twenty.[11]
These of course, are historical examples.
Many other examples are present in modern architecture.
A second, very important question concerning the architecture
today is this, "Why have contemporary architects deliberately
chosen to disregard traditional types of symmetry in their architecture?
The designs of Richard Meyer and Frank Gehry in the United States
come to mind. The advantage of examining contemporary architecture
lies in the fact that the architects are most often still living,
and while we can never ask the architect of the Pantheon why he
broke the symmetry of the rotunda, we can ask Frank Gehry why
the design of Guggenheim Museum in Bilbao apparently throws a
consideration of symmetry to the wind. I say apparently, because
I would want to ask the architect for an explanation before hazarding
any judgement of my own. So I hope in a future paper to be able
to present the fruits of this current research, and shed even
more light on the uses of symmetry, both apparent and otherwise,
in architecture.
Acknowledgments
This paper developed from a lecture I gave in April 1998 at the
Department of Mathematics of the University of Milan. I wish to
thank Simonetta di Sieno and Liliana Curcio for the invitation
to undertake this study.
Notes
1.Cf. István Hargittai and
Magdolna Hargittai, Symmetry: A Unifying Concept (Bolinas,
California: Shelter Publications, 1994). return to text
2.Cf. "The Universality of the
Symmetry Concept", Nexus: Architecture and Mathematics,
Kim Williams, ed. (Fucecchio, Florence: Edizioni dell'Erba,
1996), 81-95. return
to text
3.Cf. Dagobert Frey, "On the
Problem of Symmetry in Art" quoted in Hermann Weyl, Symmetry
(Princeton: Princeton University Press, 1989), 16. return to text
4.Cf. Sinclair Gauldie, Architecture
(London, 1969), 16. Gauldie considers the unresolved dual a "classic
and elementary" error. return
to text
5.Cf. Heinz Gotze, "Friedrich
II and the Love of Geometry", Nexus: Architecture and
Mathematics, 67-79. return
to text
6.Cf. Leonard K. Eaton, "Fractal
Geometry in the Late Work of Frank Lloyd Wright: The Palmer House",
Nexus II: Architecture and Mathematics, Kim Williams,
ed. (Fucecchio, Florence: Edizioni dell'Erba, 1998), 23-38. return to text
7.Christian Norberg-Schulz, Meaning
in Western Architecture (New York: Praeger Publishers, 1975),
145. return to text
8.Cf. Bruno Zevi, Saper vedere
l'architettura (Turin: Einaudi Editori, 1948) 57. "Impera
negli ambienti circolari e rettangolari la simmetria...una grandiosità
duplicement assiale..." ("Symmetry reigns in circular
and rectangular environments, based on dual axes..." --translation
by Kim Williams). return
to text
9.Ibid., 59. "La basilica
romana è simmetrica rispetto ai due assi: colonnati contro
colonnati, abside di fronte ad abside. Essa crea quindi uno spazio
che ha un centro preciso ed unico, funzione dell'edificio, non
del cammino umano. Che cosa fa l'architetto cristiano? Praticamente
due cose: 1) sopprime un'abside, 2) sposta l'entrata sul lato
minore. In questo modo, spezza la doppia simmetria del rettangolo,
lascia il solo asse longitudianle e fa di esso la direttrice del
cammino dell'uomo." (The Roman basilica is symmetric
with respect to the two axes: colonnade opposite colonnade, apse
opposite apse. This creates a space which has a precise and unique
center, a function of the building, not of man's movement. What
did the Christian architect do? Essentially two things: !) suppressed
an apse, 2) moves the entrance to the shorter side. Thus he breaks
the dual symmetry of the rectangle, leaving only the longitudinal
axis, which he makes the directrix of man's movement.--translated
by Kim Williams.) return
to text
10.Cf. Hermann Weyl, Symmetry,
16. return to text
11.Cf. David Speiser, "The Symmetries
of the Baptistery and the Leaning Tower of Pisa", Nexus:
Architecture and Mathematics, 135-146. return to text
Related Links
on the WWW
Nexus
Network Journal: Architecture and Mathematics Online
Chinese
Architecture: Chinese Pagodas
Sydney Opera
House
Symmetry:
Symmetry online featuring Symmetry: A Unifying Concept
by Magdolna and Istvan Hargittai
top of page
Received: 31.12.1998
 (fig.
1) with the Sydney Opera house (fig. 2)
(fig.
1) with the Sydney Opera house (fig. 2) ?
A first response might be "shape" but a more accurate
answer would be "symmetry". Each of these strange couples
of buildings share a different kind of symmetry that links them,
in spite of their temporal and cultural differences. As Magdolna
and István Hargittai have noted, symmetry, in architecture
as in other arts, is "a unifying concept".[1]
?
A first response might be "shape" but a more accurate
answer would be "symmetry". Each of these strange couples
of buildings share a different kind of symmetry that links them,
in spite of their temporal and cultural differences. As Magdolna
and István Hargittai have noted, symmetry, in architecture
as in other arts, is "a unifying concept".[1] In one, there are
an unequal number of bays; in the other, there are an equal number
of bays. The first is an example of "orthodox" bilateral
symmetry, where the facade is divided into two equal halves; but
in the second, the axis of symmetry that divides the facade into
two equal and independent halves creates a dualism. If it is true,
as Dagobert Frey maintains, that bilateral symmetry represents
"rest and binding"[
In one, there are
an unequal number of bays; in the other, there are an equal number
of bays. The first is an example of "orthodox" bilateral
symmetry, where the facade is divided into two equal halves; but
in the second, the axis of symmetry that divides the facade into
two equal and independent halves creates a dualism. If it is true,
as Dagobert Frey maintains, that bilateral symmetry represents
"rest and binding"[ Traditionally, dualism in architecture
has been considered something to be avoided. The temples of ancient
Greece, for example, always had an even number of columns so that
there was never a column on the central axis of the facade. The
avoidance of the dual by classical architects probably stems from
the ambiguity frequently attributed to the number 2, regarding
with suspicion from the time of Pythagoras. The number 2 was considered
untrustworthy (a female number) because it could be divided into
halves, in contrast to the number 3 (a male number) which was
not divisible into two parts. Even in modern architectural theory,
dualism in architecture is considered a "classical and elementary
blunder" and identified with the "amorphous or ambiguous".[
Traditionally, dualism in architecture
has been considered something to be avoided. The temples of ancient
Greece, for example, always had an even number of columns so that
there was never a column on the central axis of the facade. The
avoidance of the dual by classical architects probably stems from
the ambiguity frequently attributed to the number 2, regarding
with suspicion from the time of Pythagoras. The number 2 was considered
untrustworthy (a female number) because it could be divided into
halves, in contrast to the number 3 (a male number) which was
not divisible into two parts. Even in modern architectural theory,
dualism in architecture is considered a "classical and elementary
blunder" and identified with the "amorphous or ambiguous".[ It has a dual function: an oratory
on the ground floor and a granary above. It has an unusual two-aisled
plan. It has two altars. The difficulty of the dual on the level
of architectural experience is best exemplified by the problem
of the two altars. Where does one stand in the church? One is
forced to make a decision whether to stand in front of one altar
or the other. It is comparable to a house with two front doors.
Where is the entrance? Usually this kind of decision is made for
the spectator by the architect, who places one altar in a central
position, or one prominent front door on the facade of a house.
Thus, dualism in architecture presents a kind of a challenge to
both the spectator and the architect.
It has a dual function: an oratory
on the ground floor and a granary above. It has an unusual two-aisled
plan. It has two altars. The difficulty of the dual on the level
of architectural experience is best exemplified by the problem
of the two altars. Where does one stand in the church? One is
forced to make a decision whether to stand in front of one altar
or the other. It is comparable to a house with two front doors.
Where is the entrance? Usually this kind of decision is made for
the spectator by the architect, who places one altar in a central
position, or one prominent front door on the facade of a house.
Thus, dualism in architecture presents a kind of a challenge to
both the spectator and the architect. The Sacristy of the
basilica of S. Spirito in Florence, designed by Giuliano da San
Gallo in the last years of the fifteenth century, is octagonal
in plan and both the architecture and the distinctive pavement
design exhibit rotational and reflection (fig. 5). Domes, whether
hemispherical such as that of the Pantheon or octagonal such as
the great cupola of the Cathedral of Florence designed by Filippo
Brunelleschi, also exhibit both rotation and reflection.
The Sacristy of the
basilica of S. Spirito in Florence, designed by Giuliano da San
Gallo in the last years of the fifteenth century, is octagonal
in plan and both the architecture and the distinctive pavement
design exhibit rotational and reflection (fig. 5). Domes, whether
hemispherical such as that of the Pantheon or octagonal such as
the great cupola of the Cathedral of Florence designed by Filippo
Brunelleschi, also exhibit both rotation and reflection.  The
two opposing colonnades designed by Gianlorenzo Bernini that surround
the elliptical piazza in front of St. Peter's in Rome exhibit
chiral symmetry (fig.6). In Budapest, the two Klotid Palaces that
tower above Felszabadul<s Square, each with asymmetrically
placed towers and facade embellishments, are examples of chiral
symmetry. A very subtle form of chiral symmetry is presented by
the two leaning towers of the newly-completed Puerta de Europa
in Madrid, designed by architect John Burgee in collaboration
with Philip Johnson. Chiral symmetry in architecture is another
way to place visual emphasis on the central element of a composition.
In the case of the Puerta de Europa, for example, the two inclined
towers emphasize the broad boulevard that passes between them,
aptly forming a "gateway to Europe".
The
two opposing colonnades designed by Gianlorenzo Bernini that surround
the elliptical piazza in front of St. Peter's in Rome exhibit
chiral symmetry (fig.6). In Budapest, the two Klotid Palaces that
tower above Felszabadul<s Square, each with asymmetrically
placed towers and facade embellishments, are examples of chiral
symmetry. A very subtle form of chiral symmetry is presented by
the two leaning towers of the newly-completed Puerta de Europa
in Madrid, designed by architect John Burgee in collaboration
with Philip Johnson. Chiral symmetry in architecture is another
way to place visual emphasis on the central element of a composition.
In the case of the Puerta de Europa, for example, the two inclined
towers emphasize the broad boulevard that passes between them,
aptly forming a "gateway to Europe".  The
three are arranged in sequence: here is the beginning of the "plot"
of the story. As we enter the Pantheon, we see that the three
elements are arranged with respect to a common horizontal axis;
it is this axis that gives rise to the bilateral symmetry. However,
once inside, the horizontal axis that we have followed to gain
entrance into the rotunda disappears. It is replaced by a vertical
axis that runs from the center of the pavement up to and through
the oculus of the dome above. Thus the dominant symmetry is no
longer bilateral. The lower zone exhibits cylindrical symmetry,
while the hemispherical dome above exhibits rotation and reflection
. The reason for the change in symmetries is that, when we enter
into the rotunda we leave behind the zone of the terrestrial,
represented by the horizontal axis, and experience the zone of
the celestial, symbolized by the vertical axis. The Pantheon is
a temple dedicated to all the gods; the universe itself is represented
in the rotunda by the form of the sphere, half of which is actually
present in the coffered cupola which crowns the space, while the
other half is only made implicit in the proportions of the space
(as mentioned before, the sphere is problematic in architecture
because human beings require a horizontal plane). The sphere contains
an infinite number of planes of reflection and rotation; its infinity
symmetry makes it an apt symbol for the cosmos.
The
three are arranged in sequence: here is the beginning of the "plot"
of the story. As we enter the Pantheon, we see that the three
elements are arranged with respect to a common horizontal axis;
it is this axis that gives rise to the bilateral symmetry. However,
once inside, the horizontal axis that we have followed to gain
entrance into the rotunda disappears. It is replaced by a vertical
axis that runs from the center of the pavement up to and through
the oculus of the dome above. Thus the dominant symmetry is no
longer bilateral. The lower zone exhibits cylindrical symmetry,
while the hemispherical dome above exhibits rotation and reflection
. The reason for the change in symmetries is that, when we enter
into the rotunda we leave behind the zone of the terrestrial,
represented by the horizontal axis, and experience the zone of
the celestial, symbolized by the vertical axis. The Pantheon is
a temple dedicated to all the gods; the universe itself is represented
in the rotunda by the form of the sphere, half of which is actually
present in the coffered cupola which crowns the space, while the
other half is only made implicit in the proportions of the space
(as mentioned before, the sphere is problematic in architecture
because human beings require a horizontal plane). The sphere contains
an infinite number of planes of reflection and rotation; its infinity
symmetry makes it an apt symbol for the cosmos.
