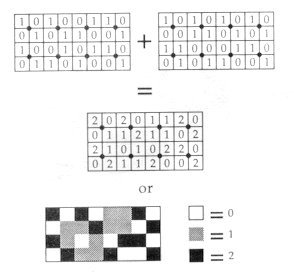
Figure 29.
As Lunda-designs may be considered as matrices,
it is quite natural to define addition of Lunda-designs
in terms of matrix addition: the sum of two (or more)
matrices (of the same dimensions) is the matrix in which the
elements are obtained by adding corresponding elements
(see the example in Figure 29).
The sum of k mxn Lunda-designs may be called a
mxn Lunda-k-design. The Lunda-k-designs inherit
the following symmetry properties:
(i) The sum of the elements in any row is equal to km;
(ii) The sum of the elements in any column is equal to kn;
(iii) The sum of the integers in two border unit squares of
any grid point in the first or last rows or columns is equal to k;
(iv) The sum of the integers in the four unit squares between two
arbitrary (vertical or horizontal) neighbour grid points is always 2k.
Once again, properties (i) and (ii) guarantee a
global equilibrium for each row and column.
Properties (iii) and (iv) guarantee more local equilibria.
The characteristics (i), (ii), (iii), and (iv) may be
used to define Lunda-k-designs of dimensions mxn.
The characteristics (iii) and (iv) are sufficient for
this definition, as they imply (i) and (ii).


Figure 30.

Figure 31.

Figure 32.
Figure 30 displays the forty 3x3 Lunda-3-designs of
the type d4', with white
( = 0) being the
colour of the first unit square (with vertices (0,0), (1,0), (1,1), and (0,1)).
Figure 31 shows an example of a 8x8 Lunda-4-design.
Figure 32 displays examples of a 4x4 Lunda-5-design, an 8x4
Lunda-5-design, and a 5x3 Lunda-4-design. This time the colour chosen
for the first unit square is different from white.