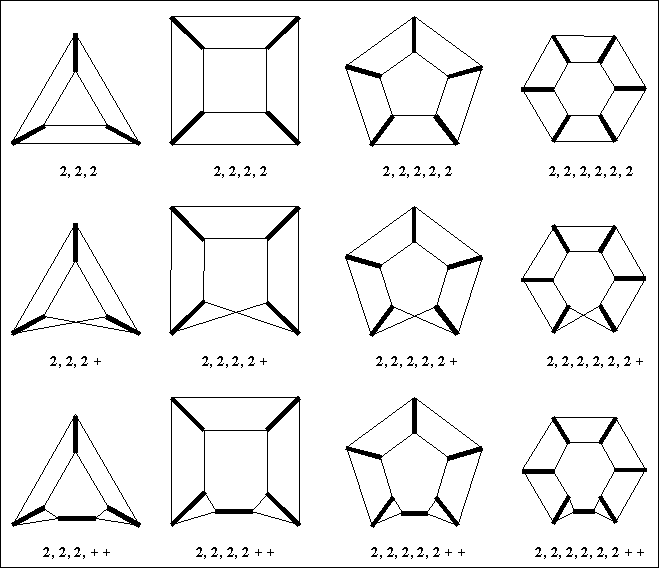

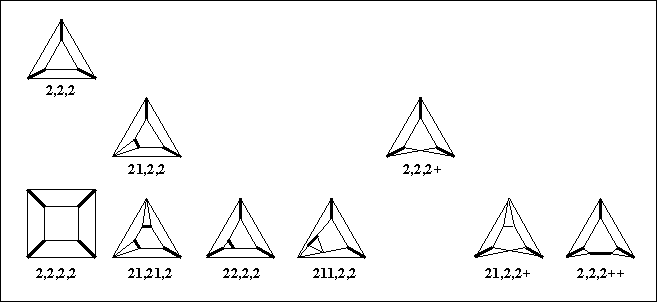
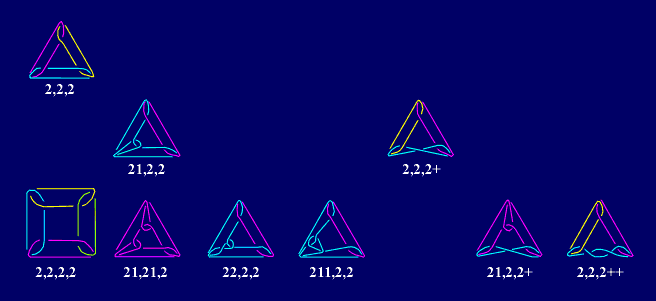
|
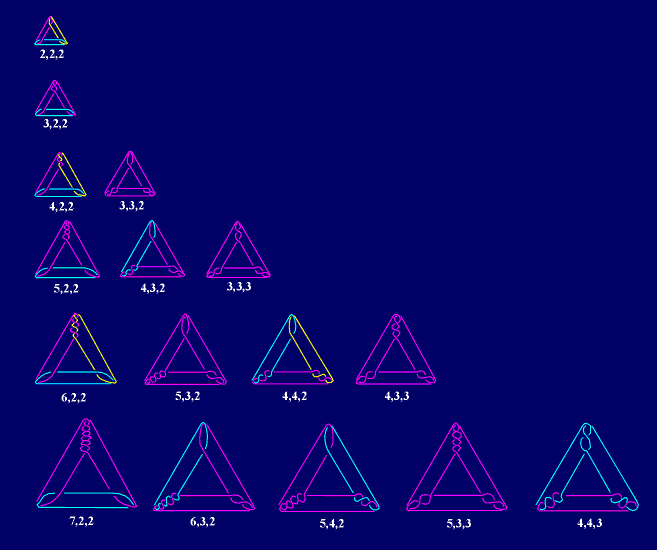
In the family p,q,r (p ³ q ³ r ³ 2) we have three-component links for p = q = r = 0 (mod 2), two-component links if exactly one of the numbers p,q,r is odd, and knots if at least two of them are odd. All the properties of the links obtained are regularly distributed: their Alexander polynomials, unknotting numbers, etc. For example, for the knots from this family we have the following abbreviated Alexander polynomials and unknotting numbers: 3,3,2 1-3+4-5 2 5,3,2 1-3+4-5+5 3 7,3,2 1-3+4-5+5-5 4 9,3,2 1-3+4-5+5-5+5 5 3,3,3 7-13 3 5,3,3 10-19 3 7,3,3 13-25 3 9,3,3 16-31 3 4,3,3 2-5+6-7 3 6,3,3 3-7+8-9 3 8,3,3 4-9+10-11 3 |