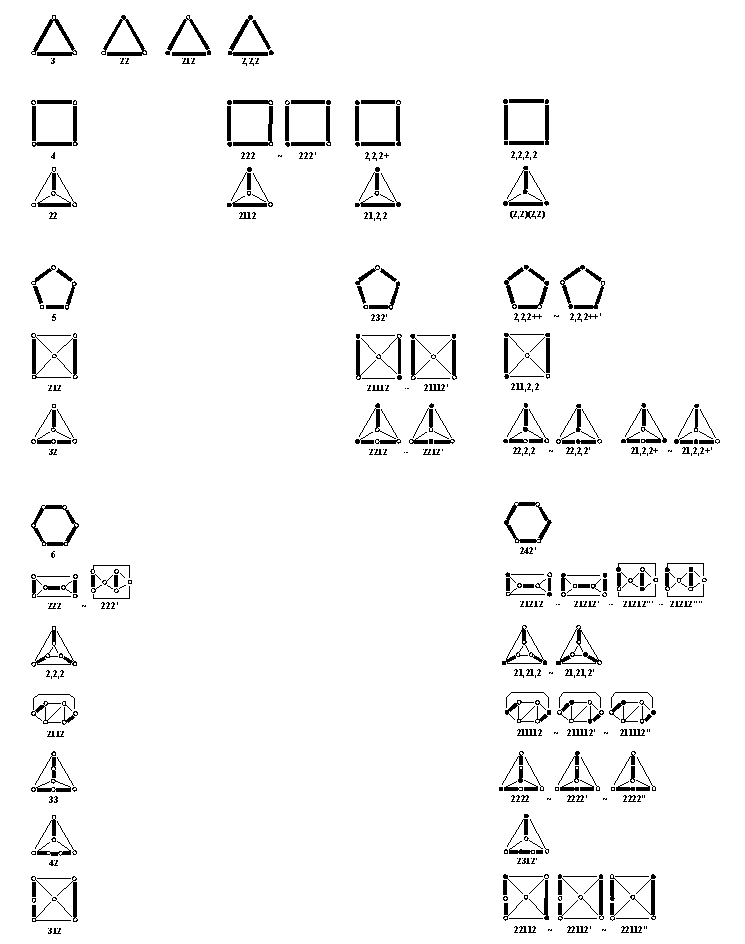
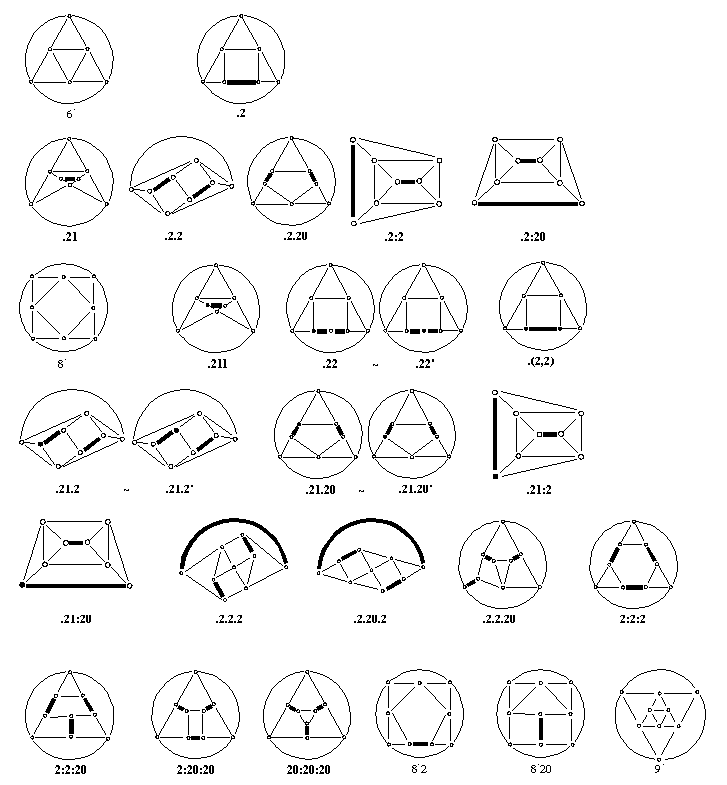
3₁   3               4 6 2                          1 0  3
4₁   22             4 6 8 2                       1 0 -2  0
5₁   5               6 8 10 2 4                  1 0  5  0   5
5₂   32             4 8 10 2 6                  1 0  1  0   5
6₁   42             4 8 12 10 2 6             1 0 -4 -2  3  2
6₂   312           4 8 10 12 2 6             1 0  1 -1 -3  2
6₃   2112         4 8 10 2 12 6             1 0  2  0  3   0
7₁   7               8 10 12 14 2 4 6        1 0  7  0 14  0  7
7₂   52             4 10 14 12 2 8 6        1 0 -3  0 -2  0  7
7₃   43             6 10 12 14 2 4 8       -1 0 -1  0  8  0  7
7₄   313           6 10 12 14 4 2 8        1 0 -4  0  2  0  7
7₅   322           4 10 14 12 2 6 8       -1 0 -2  1  4  0  7
7₅'   322'          4 10 12 14 2 8 6       -1 0 -3  0  4  0  7
7₆   2212         4 8 12 2 14 6 10         1 0 -1 -1 -1 -2 3
7₆'   2212'        4 8 12 10 2 14 6       -1 0  0 -1  3 -1  3
7₇   21112       4 8 10 12 2 14 6         1 0 -1 -1 -1 -2 3
7₇'   21112'     4 8 12 10 2 14 6        -1 0   0 -1  3 -1 3

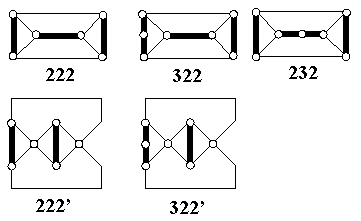
Among them, to the amphicheiral projections of 4₁ (22) and 6₃ (21²2) correspond even polynomials [46].

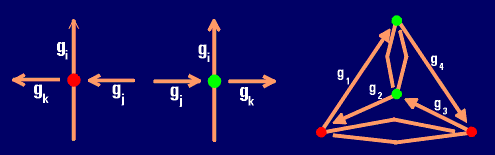
Liang polynomial A(t) [28] is defined by the similar determinant, where a_ii = t^e, and a_ij = s if the vertices i, j are connected with the multiplicity s (s = 0,1,2). In this case, for the amphicheiral knot projections A(t) = A(t ^-1). For example, for the amphicheiral knot 4₁ (22) we have A(t) = A(t ^-1) = -4t²+8t-3+8t ^-1-4t ^-2.