We describe, in this section, two iterative folding procedures that may be used on your gummed tape to fold strips of equilateral triangles and strips which can be used to construct regular pentagons. In both of these cases the procedure is a convergent one so that the angles you produce on the tape become more and more regular as you continue to fold. You will also need to fold a strip of consecutive squares (but this is an exact construction that we feel confident you can do on your own).

To fold the equilateral triangles simply follow the instructions in the numbered frames of Figure 1.

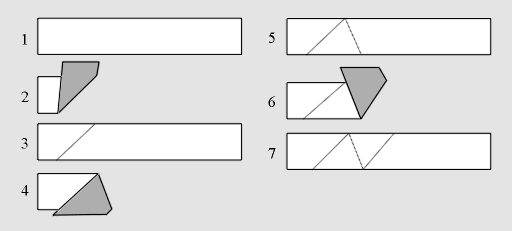
Figure 1: 1) Begin with a long strip of gummed tape; 2) Fold UP - any way will do; 3) Unfold; 4) Fold DOWN - now you must do it exactly as shown; 5) Unfold; 6) Fold UP, exactly as shown; 7) Unfold.

Now go to frame 4, and keep repeating the folding in frames 4 through 7, to make a string of triangles as long as you need. Notice two things. First, the folding procedure, after your initial fold, goes DOWN, UP, DOWN, UP,... We will abbreviate this folding procedure by D¹U¹ and call the tape produced the D¹U¹-tape. ² Second, you can readily see that, as we claimed, the triangles become more and more regular as you fold. Thus, if you wish to use this tape to construct models requiring equilateral triangles, all that you need to do is compare successive triangles, beginning with the first one formed, until it is not possible to detect any difference between them - and then throw away the defective ones and continue to fold, in the prescribed manner, to obtain the equilateral triangles you need for the constructions in Section 3. (We show in [Math] how to prove that all angles on this tape do, in fact, approach p/3.)

To fold tape from which you can construct regular pentagons simply follow the instructions in the numbered frames of Figure 2.

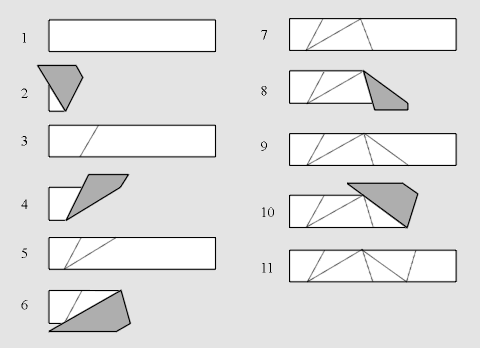
Figure 2: 1) Begin with a long strip of gummed tape; 2) Fold UP - any way will do; 3) Unfold; 4) Fold DOWN - now you must do it exactly as shown; 5) Unfold; 6) Fold UP, exactly as shown; 7) Unfold; 8) Fold DOWN, exactly as shown; 9) Unfold; 10) Fold UP, exactly as shown; 11) Unfold.

Now go to frame 4, and keep repeating the folding in frames 4 through 11, to make a string of tape from which you will be able to construct regular pentagons. First, notice that the folding process, after the first two initial folds, goes DOWN, DOWN, UP, UP, DOWN, DOWN, UP, UP,... We will abbreviate this folding procedure by D²U² and call the tape produced the D²U²-tape. Second, notice that this tape has two kinds of crease lines, which we will refer to as short and long crease lines. Third, it is evident that the configuration formed by these crease lines is becoming more and more regular, reproducing the same angles at each edge of the tape. (We show in [Math] how to prove that the smallest angles on this tape do, in fact, approach p/5.)

This is the tape that you will use to make regular pentagons and models with regular pentagonal faces. To see how this works throw away the first few triangles you have folded (10 will be very safe) and continue to fold, in the prescribed manner, to obtain the tape you need to produce the constructions in Section 3. Just to practise now, cut off a piece of tape and make the pentagon shown in Figure 3. Notice that when you constructed this pentagon you cut the D²U²-tape along a short crease line, and folded on short crease lines.

Figure 3: Make a section of tape that looks like this (1), into a pentagon that looks like this (Shading indicates the other side of the tape).

What about the long crease lines? Try cutting along a long crease line and folding on successive long crease lines to construct the pentagon shown in Figure 4 (of course you will also have finally to cut along another long crease line to complete the model as it is shown).

Figure 4: The end of the tape must be tucked in here (red arrow).

---