|
Recall how much pleasure we took in the fact that the diagonal cube and the
golden dodecahedron retained all their inherent symmetry. Generally
speaking, braided models lose some of the symmetry of the underlying
geometric figure; indeed, our braided tetrahedron, octahedron and icosahedron
all lost some of the underlying geometric symmetry. Thus it is natural to
ask "Is it possible to braid the tetrahedron, octahedron and icosahedron in
such a way as to retain all the symmetry of the original polyhedron?"
We have recently discovered a way to do this. The problem was to design
strips so that three strips cross over each other to form each (triangular
face) in a symmetric way.
Figure 18(b) shows a typical
straight strip of 5 equilateral triangles
with a slit in each triangle from the top (or bottom) edge to (just past) the
center.8
The perfect tetrahedron is constructed out of Figure 18(a)
where you will
see how the 3 strips are interlaced initially. We leave the
completion of the model as a challenge to you.
Figure 19(a) shows the layout of 3
strips for the beginning of the
construction of the perfect octahedron.
We'll give you one more hint. When you use Figure 19(a)
remember that the strip shown below it in Figure 19(b)
has to be braided into the figure above it.
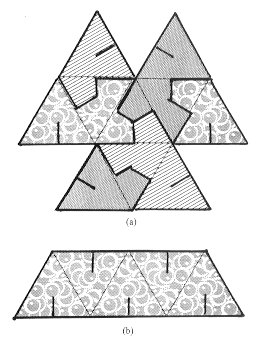
Figure 18
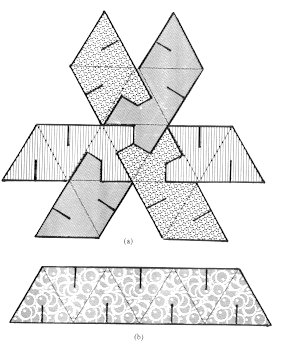
Figure 19
A perfect icosahedron may be constructed from 6 strips of this type
having 11 triangles on each strip. Over to you! But take heart -
these models take several hours to construct. Just to prove that they
really do exist we show the photo of them in Figure 20.

Figure 20
8
Theoretically the slit could go just to the center, but the model is then
impossible to assemble. You need to have some leeway for the pieces to be
free to move during the process of construction - although they will
finally land in a symmetric position so that it looks as though the slit need
not have gone past the center.
|