Let X be a finite set; the reader might like to keep in mind the set of vertices (or edges, or faces) of a polygon or polyhedron; and let G be a finite symmetry group acting on X. Suppose X has n elements, and that G has m elements; we write |X| = n, |G| = m. We may represent the elements of the set X by the integers 1,2,...,n. If g Î G, then g acts as a permutation of {1,2,...,n}. Now every permutation is uniquely expressible as a composition of cyclic permutations on mutually exclusive subsets of the elements of X. For example, the permutation

is the composite (1 2 4)(3 7 5)(9 8 6 11)(10), where, e.g., (1 2 4) denotes the cyclic permutation

Thus the permutation (5.1) is the composite of one cyclic permutation of length 1, two cyclic permutations of length 3, and one cyclic permutation of length 4, the cyclic permutations acting on disjoint subsets of the set X. In general a permutation of X has the type (a₁, a₂,...,a_n} if it consists of a₁ permutations of length 1, a₂ permutations of length 2,..., a_n permutations of length n, the permutations having disjoint domains of action; notice that å_{i = 1} ⁿa_i = n. For example the permutation (5.1) has the type {1,0,2,1,0,0,0,0,0,0,0}. If g has the type {a₁,a₂,...,a_n}, we define the cycle index of g to be the monomial

The cycle index of G is Z(g) = ( å_{g Î G}Z(g) )/m.

Example 5.1 We consider the symmetries of the square as shown in Figure 8.

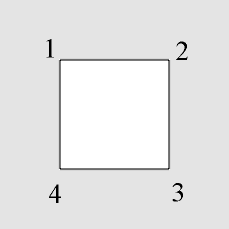
Figure 8: We denote this labeling of the square by 1234.

The group G of symmetries is a group of order 8, which we describe by permutations of the set of vertices {1,2,3,4}. Thus

g₁ (Identity) (1 2 3 4) (1 2 3 4)      (cycle index x₁⁴ )
g₂               (1 2 3 4) (2 3 4 1)      (cycle index x₄ )
g₃               (1 2 3 4) (3 4 1 2)      (cycle index x₂² )
g₄               (1 2 3 4) (4 1 2 3)      (cycle index x₄ )
g₅            (1 2 3 4) (3 2 1 4)      (cycle index x₁²x₂ )
g₆            (1 2 3 4) (1 4 3 2)      (cycle index x₁²x₂ )
g₇               (1 2 3 4) (2 1 4 3)      (cycle index x₂² )
g₈               (1 2 3 4) (4 3 2 1)      (cycle index x₂² )

Thus the cycle index of G is (x₁⁴+2x₁ ²x₂+3x₂²+2x₄)/8.

Now suppose we want to color the elements of X; that is, we have a finite set Y of colors, |Y| = r, and a coloring of X is a function ⁴ f: X ® Y. For any g Î G, we regard the colorings f and fg as indistinguishable or equivalent; and a pattern is an equivalence class of colorings. Then Pólya's first theorem is as follows.

Theorem 5.1: The number of patterns is Z(G;r,r,...,r).

Example 5.1: (continued) Suppose the vertices are to be colored red or blue. Then r = 2, and the number of patterns is (16+16+12+4)/8 = 6. In fact, the patterns are represented by the 6 colorings: RRRR, BRRR, BBRR, BRBR, RBBB, BBBB,

We now describe Pólya's second theorem. This is really the 'big' theorem and the first theorem is, in fact, deducible from it. Let us enumerate the elements of Y (the 'colors') as y₁,y₂, ...,y_r.

Theorem 5.2: Evaluate Z(G;x₁,x₂, ...,x_n) at x_i = å_{j = 1}^ry_jⁱ. Then the coefficient of y₁^n₁y₂^n₂ ...y_r^n_r is the number of patterns assigning the color y_j to n_j elements ⁵.

Example 5.1: (continued) For the symmetries of the square we know that

Thus if Y = {R,B}, then the evaluation of Z(G) at x_i = Rⁱ+Bⁱ yields

(It is, of course, no coincidence that this polynomial is homogeneous (of degree |X| and symmetric. Thus the Pólya Enumeration Theorem tells us that there is one pattern with 4 red vertices (obvious); one pattern with 3 red vertices and 1 blue vertex, represented by the coloring RRRB; 2 patterns with 2 red vertices and 2 blue vertices, represented by the colorings BRRB and RBRB, and the remaining possibilities are analyzed by considerations of symmetry.)

Now, given a pattern, there are the various functions fg : X ® Y, where f is a fixed coloring and g Î G, in that equivalence class of colorings. These are the homologues, or, more precisely, the homologues of f. Let us revert to our example.

Example 5.1: (continued) As we have seen, there is one coloring in which all vertices are colored red. There is only one homologue, namely RRRR,

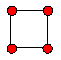
There is one coloring in which 3 vertices are colored red and one blue. There are 4 homologues, namely BRRR, RBRR, RRBR, RRRB,

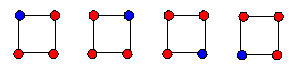
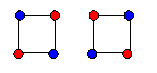
where one vertex is colored blue. There are two colorings in which 2 vertices are colored red and 2 blue. In the first there are 4 homologues, namely BBRR, RBBR, RRBB, BRRB,

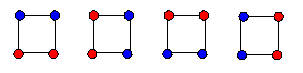
In the second there are 2 homologues, namely BRBR, RBRB,

The analysis is completed by considerations of symmetry.

Let us show how this conception of homologues agrees with our earlier definition. We are given the group G of permutations of X. Given a coloring f: X ® Y, we consider the subset G₀ of G consisting of those g such that fg = f, that is, those movements of X which preserve the coloring. It is easy to see (just as easy as in our earlier, simpler situation) that G₀ is a subgroup of G. Corresponding to each coset G₀g of G₀ in G we have a coloring fg of X and these colorings run through the pattern determined by f. We have described the set of colorings {fg} as the set of homologues of the coloring f; as indicated earlier, they are in one-one correspondence with the cosets of G₀ in G.