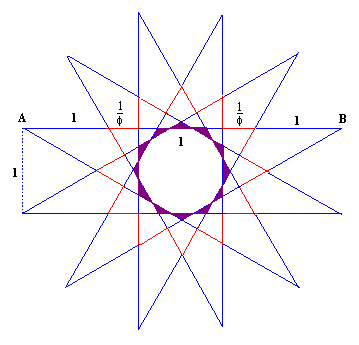
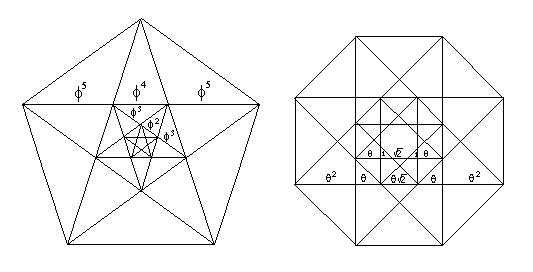
Figure 1. a) Diagonals of a star pentagon intersect in the golden ratio (f :1); b) diagonals of a star octagon intersect in the sacred cut ratio (1 +Ö 2 : 1); c) diagonals of a 12-pointed star intersect in the ratio of 1+Ö 3:1. |
|
The proportions relevant to a system of proportionality make their appearance as a pair of ratios: 1) the ratio in which the edges of a regular star polygon intersect, and 2) the ratio of the longest diagonal of a regular polygon to the length of the side. A star polygon with n vertices in which each vertex connects to the p-th vertex rotated from it in a clockwise direction is denoted by {n,p}. If n and p are relatively prime, the star polygon can be drawn in a single stroke without taking pencil off paper. In Figure 1a the edges of a star pentagon {5,2} intersect each other in the golden section f : 1 while the ratio of diagonal to edge length of a regular pentagon is also f : 1. In Figure 1b the edges incident to consecutive vertices of the star octagon {8,3} intersect in the ratio of q : 1 where q = 1 + Ö 2 while the ratio of diagonal to edge of the octagon is also q : 1. The proportions of the root 3 system are determined by the intersection of consecutive edges of a star dodecagon {12,5} which intersect in the ratio y : 1 where y = 1 + Ö 3. The ratio of the longest diagonal to the edge of a dodecagon is b : 1 where b = 2 + Ö 3 = y 2/2. This presents a second proportion of importance to the root 3 system. |


Figure 1. a) Diagonals of a star pentagon intersect in the golden ratio (f :1); b) diagonals of a star octagon intersect in the sacred cut ratio (1 +Ö 2 : 1); c) diagonals of a 12-pointed star intersect in the ratio of 1+Ö 3:1. |