SPECIAL CLASSES
              OF
LUNDA-DESIGNS

Figure 16.

Especially attractive are Lunda-designs which display extra symmetries. Figure 16 presents the six possible 3x3 Lunda-designs (being white (= 0) the colour of the first unit square with vertices (0,0), (1,0), (1,1), and (0,1)), which admit reflections in the diagonals that preserve the colours and vertical and horizontal reflections interchanging black and white. By consequence, a half-turn about the centre preserves the colours and a quarter-turn reverses the colours. Abreviately, these finite designs are of the type d4' (for this notation, see e.g. Washburn & Crowe, p. 68).

Figure 18.

Figure 19.

Figure 17 displays the 18 4x4 Lunda-designs and Figure 18 the 84 5x5 Lunda-designs which have the same symmetries. Figure 19 presents examples of mirror designs which generate such 5x5 Lunda-designs (the numbers indicate the corresponding Lunda-designs in Figure 18).

When we join four Lunda-designs of the type d4', a new Lunda-design of the same type is obtained (see the example in Figure 20).

Figure 21 displays examples of 5x5 Lunda-designs - together with corresponding generating mirror designs, which, although they do not have symmetry axes, do possess the property that a quarter-turn about the respective centre reverses the colours, and consequently a half-turn preserves the colours (type c4').

Figure 23.

Figure 24.

Figure 25.

Figure 26.

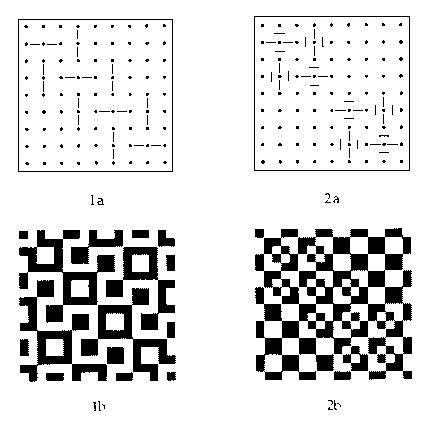
Figure 22 presents examples of 9x9 Lunda-designs of the type d4' together with corresponding generating mirror designs. Figure 23 does the same for 7x7 Lunda-designs of the type c4'. Examples of 9x9 and 13x13 Lunda-designs of the same type c4' are displayed in Figures 24 and 25. Two examples of 9x9 Lunda-designs which admit reflections in their diagonals are given in Figure 26.