
|
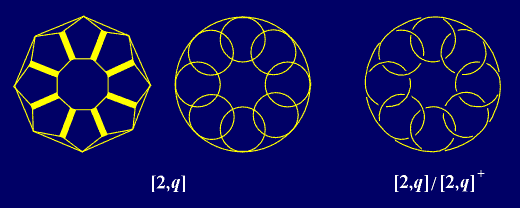
Symmetry groups of knots, that is, groups of isometries that map the knot onto itself, are considered by B.Grünbaum and G.C.Shephard [20]. From the 14 kinds of point groups in E3 [21], as the symmetry groups of knots can occur [q], [q]+, [2,q]+, [2+,2q], {2+,2q], [2,¥], [2,q] and [2,q+], where q is a positive integer. For every alternating knot we could distinguish the graph symmetry group G, and its subgroup G' of the index 2, obtained by alternating. |