

|
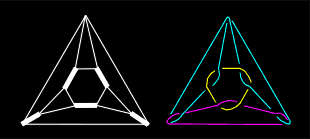
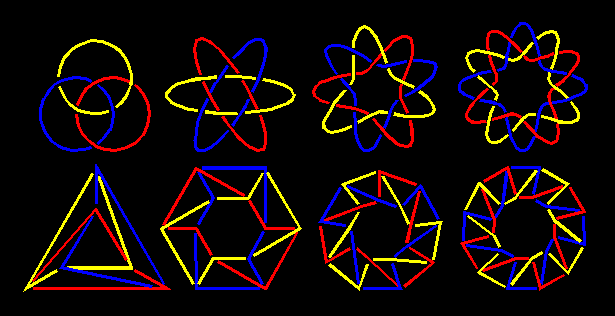
"No two elements interlock, but all three do interlock". Such a three-component link is named "Borromean rings" after the Borromeas, an Italian family from the Renaissance that used them as their family crest symbolizing the value of collaboration and unity. Borromean circles are impossible: B.Lindström and H.O.Zetterström [39] proved using geometrical arguments that three flat circles cannot be Borromean, but that Borromean triangles are possible. The Australian sculptor J.Robinson assembled three flat hollow triangles to form a structure (called Intuition), topologically equivalent to Borromean rings. Their cardboard model collapses under its own weight to form a planar pattern. P.Cromwel has found it as the detail from the picture-stone from Gotland [40]. This and other symmetrical combinations of three and four hollow triangles are considered by H.S.M.Coxeter [41]. Borromean rings you could find in geometry as the regular octahedron {3,4}, in Venn diagrams, in DNA, and in other various areas. |
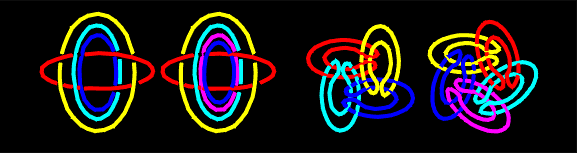
|
In the knot theory Borromean rings are the first link with two remarkable properties: three mutually disjoint simple closed curves form a link, yet no two curves are linked, and if any one curve is cut, the other two are free to separate. In the case of 3-component links that two properties are inseparable: one follows from the other. In the case of n-component links (n > 3) we could define n-Borromean links as n-component nontrivial links such that any two components form a trivial link. Among them, we could distinguish those with at least one nontrivial sublink, for which we will keep the name "Borromean links", and Brunnian links in which every sublink is trivial [42]. |
|
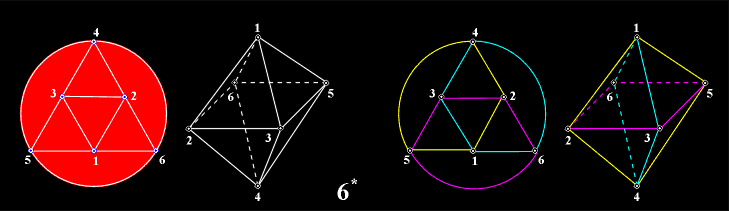
It seams surprising that after the Borromean rings, represented by the link 623 in Rolfsen notation, in link tables you cannot find any other link with the mentioned properties [16]. The reason for this is very simple: all existing knot tables contain just the links with at the most 9 crossings. In fact, there is an infinite number of Borromean or Brunnian links, and they could be derived as infinite series. The first such series of 3-component links, beginning with the Borromean rings, is discovered by P.G.Tait [43]. It is easy to recognize their geometrical source: as the limiting case for n = 1 we have the regular octahedron {3,4}, and for n > 1 the series of (3n)-gonal antiprisms. By alternating, from their corresponding 4-regular graphs (or Schlegel diagrams) we obtain the series of achiral 3-Borromean links. |
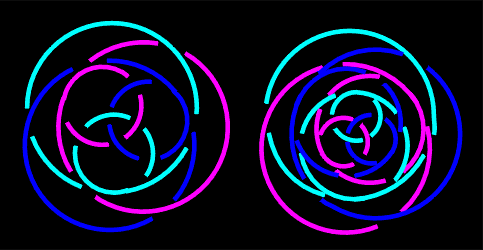
|
Some other infinite series of Borromean links from my paper "Are Borromean links so rare?" (to appear). |