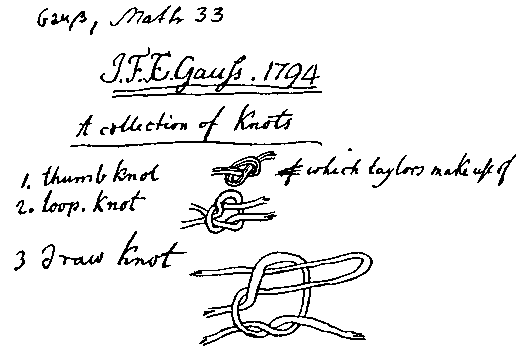
|
Every link could be represented by its regular projection
(diagram, or simply, a shadow), where the "regular" means that
projections of vertices or edges cannot be incident. To every link
correspond one or more minimal (reduced) nonisomorphic projections, i.e. the
projections with a minimum number of crossings. In the case of alternating knots,
minimal projections are always alternating.
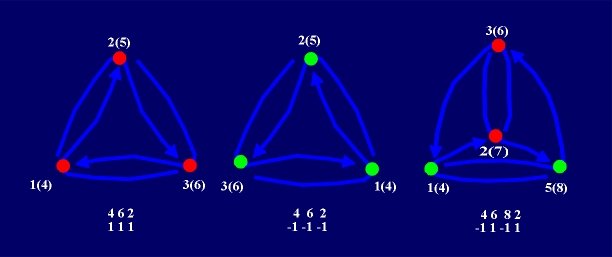
Labeling the crossings of an oriented reduced knot projection, we obtain the
Gauss code or Dowker code of this projection. For example,
Gauss code of the trefoil is ABCABC. In Dowker code,
every crossing point is labeled by two numbers, one even and the other
odd. For every projection, it is sufficient to know the corresponding
permutation of even numbers, followed by signs of crossing points.
Hence, to the right trefoil corresponds Dowker sequence 4 6 2 and
the sequence of signs 1 1 1, to the left trefoil the same sequence 4 6 2
and the sequence of signs -1 -1 -1, to the figure-eight
knot the sequences 4 6 8 2 and -1 1 -1 1, or 6 8 2 4 and -1 1 -1 1, etc., where
4 6 8 2 is a shorthand for:
4 6 8 2 If we are not interested for the orientation of an alternating knot, only Dowker sequence is sufficient. Dowker code is dependent from the choice of the beginning point, so the same projection could be described by different Dowker codes. Hence, for every reduced projection we take its first (minimal) Dowker code, and for every knot the minimal Dowker code of all its reduced projections [11]. |