Tetrahedron: Lay one strip over the other strip (with the colors not showing) exactly as shown in Figure 13(a). Think of the triangle ABC as the base of the tetrahedron; for the moment the triangle ABC remains fixed. Then fold the bottom strip into a tetrahedron by lifting up the two triangles labeled X and overlapping them so that C ¢ meets C, B¢ meets B, and D¢ meets D. Don't worry about what is happening to the other strip as long as it stays in contact with the bottom strip where the two triangles originally overlapped. Now you will have a tetrahedron with three triangles sticking out from one edge. Complete the model by wrapping the protruding strip around two faces of the tetrahedron (with the color showing) and tucking in the last triangle so that it looks like Figure 13(b).

Figure 13

Hexahedron (cube): First take one strip and clip it together so that the color is outside and the end squares fit over each other. Do the same with a second strip. Slip one of these over the other so that the holes of the cube are all covered and so that the overlapping squares of the second strip do not cover any squares from the first strip, and so that the paper clip on the first strip is covered as shown in Figure 14(a). Now slide the third strip underneath the top square so that two squares from the third strip stick out on both the right and left sides of the cube, as shown in Figure 14(b). Turn the model upside down and tuck in the ends of this strip to form Figure 14(c). You may remove the paper clips before you complete the construction; but, when you become really adept, you'll find you don't need the paper clips at all.

Figure 14

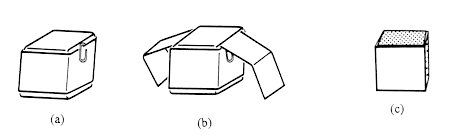
Octahedron: Begin with a pair of overlapping strips held together with a paper clip, as indicated in Figure 15(a) (with the color visible). Fold these two strips into a double pyramid by placing triangle a₁ under triangle A₁, triangle a₂ under triangle A₂, and triangle b under triangle B. Secure the overlapping triangles b, B with a paper clip to produce the configuration shown in Figure 15(b). Repeat this process with the other two strips. Then place the second pair of braided strips over the first pair, as shown in Figure 15(c). When doing this, make certain the flaps with the paper clips are oriented precisely as shown in the figure. Now, pick up the entire configuration and complete the octahedron by moving the pyramids together as shown by the arrow marked 1. Performing step 2 simply places the flap with the paper clip on it against a face of the octahedron. In step 3 you wrap the remaining portion around the octahedron and tuck the last flap (with a paper clip on it) inside the model. Again, when you become adept at this process you will be able either to do it without paper clips, or, at least, to slip the paper clips off just before you perform the last three steps. Actually this is just an aesthetic consideration, since the paper clips won't be visible on the completed model.

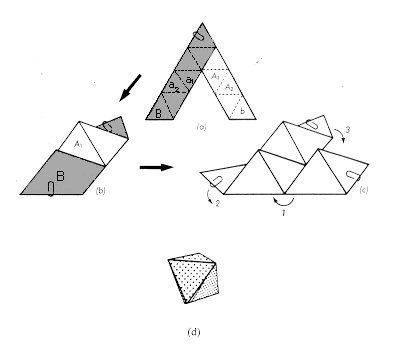
Figure 15

Icosahedron: Label each of triangles on one of the strips with a 1 on the uncolored side of the tape. Then label the next strip with a 2 on each of its triangles, the next with a 3 on each of its triangles, the next with a 4 on each of its triangles, and, finally, the last with a 5 on each of its triangles.

Now lay the 5 strips out so that they overlap each other precisely as shown in Figure 16(a), making sure that the center 5 triangles form a shallow cup that points away from you. You may wish to use some transparent tape to hold the strips in this position.

Now study the situation carefully before making your next move. You must bring the 10 ends up so that the part of the strip at the tail of the arrow goes under the part of the strip at the head of the arrow (this means "under" as you look down on the diagram, because we are looking at what will become the inside of the finished model). Half the ends wrap in a clockwise direction, and the other end of each strip wraps in a counterclockwise direction. What finally happens is that each strip overlaps itself at the top of the model. In the intermediate stage it will look like Figure 16(b). At this point it may be useful to put a rubber band (not too tight) around the emerging polyhedron just below the flaps that are sticking out from the pentagon. Then lift the flaps as indicated by the arrows in Figure 16(b) and bring them toward the center so that they tuck in as shown in Figure 16(c).

The model is completed by first lifting flap 1 and smoothing it into position. Then you should do the same with flaps 2, 3 and 4. Finally, flap 5 will tuck into the obvious slot and you will have produced the model shown in Figure 16(d).

This model is, in the view of the authors, the most difficult of the 9 puzzles to construct and it is not very stable. You might want to put a couple of lightweight rubber bands around it to prevent it from falling apart when it is handled.

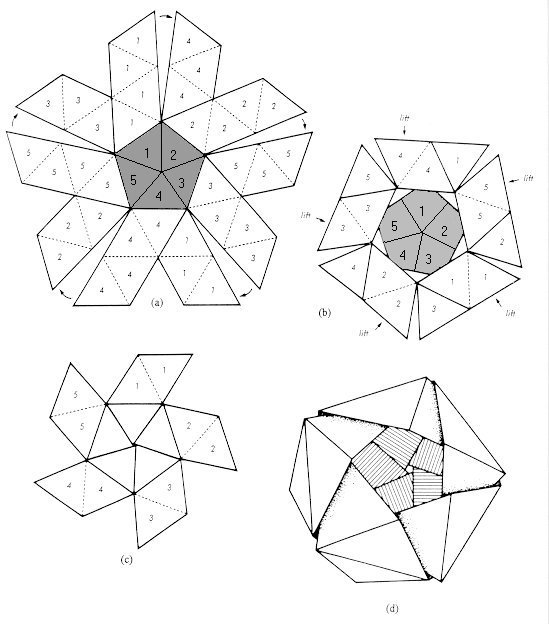
Figure 16

Dodecahedron: Take two of the strips and secure them with a bobby pin as shown in Figure 17(a) (with the colored side visible).⁷ Then make a bracelet out of each of the strips in such a way that
(a) four sections of each strip overlap, and
(b) the strip that is under on one side of the bracelet is over on the other side. (This will be true for both strips.)

Use another bobby pin to hold all four thicknesses of tape together on the edge that is opposite the one already secured with a bobby pin.

Repeat the steps above with another pair of strips. You will then have two identical bracelet-like arrangements. Slip one inside the other one as illustrated in Figure 17(b), so that it looks like a dodecahedron with triangular holes on four of its faces.

Next take the last two strips and cross them precisely as you did in Figure 17(a) (to do otherwise would destroy some of the symmetry); then secure them with a bobby pin. Carefully put two of the loose ends (either the top two or the bottom two) through the top hole and pull them out the other side so that the bobby pin lands on CD. Then put the other two ends through the bottom hole and pull them out the other side. Now you can tuck in the loose flaps, but make certain to reverse the order of the strips - that is, whichever one was on the bottom at CD should be on the top when you do the final tucking.

After you have mastered this construction you may wish to try to construct the model with tricolored faces, shown in Figure 17(e), which illustrates, rather vividly, exactly how to inscribe the cube symmetrically inside the dodecahedron. You may also note a similarity between this construction and the cube of Figure 10.

Figure 17

---