We agreed in [Rec] that, however symmetry is defined, the most symmetric polygons are the regular polygons, both the regular convex polygons and the regular star polygons (see [C1] ). This is our justification for devoting this section to a particularly easy way of constructing examples of such polygons; in fact, we will confine ourselves, in this article, to the construction of regular convex polygons. The practical problems of such constructions are discussed in our companion article [Rec].

To set our problem in its historical context, we should really begin with the Greeks and their fascination with the challenge of constructing regular convex polygons. We will refer to such p-sided polygons as regular convex p-gons, and we may even suppress the word convex if no confusion would result. The Greeks, working on these problems about 350 B. C., restricted themselves to constructions using only what we call Euclidean tools, namely an unmarked straightedge and a compass. No doubt the Greeks would have liked to be able to describe Euclidean constructions whenever possible. However, they were only able to provide such constructions for regular convex polygons having p sides, where

About 2,000 years later Gauss (1777 - 1855) showed that Euclidean constructions were possible only rarely. He proved that a Euclidean construction is possible if and only if the number of sides p is of the form p = 2^cÕr_i, where the r_i are distinct Fermat primes - that is, primes of the form F_n = 2²ⁿ+1.

Gauss's discovery was remarkable - it tells us precisely which regular p-gons admit a Euclidean construction, provided, of course, that we know which Fermat numbers F_n are prime. In fact, not all Fermat numbers are prime. Euler (1707 - 1783) showed that F₅ = 2²⁵+1 is not prime, and although many composite Fermat numbers have been identified, to this day the only known prime Fermat numbers are

Thus, even with Gauss's contribution, there exists a Euclidean construction of a regular p-gon for very few values of p, and even for these p we do not in all cases know an explicit construction. For example, in The World of Mathematics [N] we read:

Simple Euclidean constructions for the regular polygons of 17 and 257 sides are available, and an industrious algebraist expended the better part of his years and a mass of paper in attempting to construct the F₄ regular polygon of 65,537 sides. The unfinished outcome of all this grueling labor was piously deposited in the library of a German university .

Despite our knowledge of Gauss's work we still would like to be able to construct (somehow) all regular p-gons. Our approach is to redefine the question so that, instead of exact constructions, we will ask for which p ³ 3 is it possible, systematically and explicitly, to construct an arbitrarily good approximation to a regular p-gon? We take it as obvious that we can construct a regular p-gon exactly if p is a power of 2. What we will show is that it is possible, simply and algorithmically, to construct an approximation (to any degree of accuracy) to a convex p-gon for any value of p ³ 3. In fact, we will give explicit (and uncomplicated) instructions involving only the folding of a straight strip of paper tape in a prescribed periodic manner.

Although the construction of regular convex p-gons would be a perfectly legitimate goal by itself, the mathematics we encounter is generous and we achieve much more. In the process of making what we call the primary crease lines used to construct regular convex p-gons we obtain tape which can be used to fold certain (but not all) regular star polygons. It is not difficult to add secondary crease lines in order to obtain tape that may be used to construct the remaining regular star polygons.

As it turns out, the mathematics we encounter, in validating our folding procedures, leads quickly and naturally to questions, and hence to new results, in number theory. Those interested may consult [HP3]. In the interests of mathematical simplicity, as we have said, we will confine attention, in this article, to convex polygons. The more ambitious reader, interested in star polygons, may consult [C1, HP2, 3].

Let us begin by explaining a precise and fundamental folding procedure, involving a straight strip of paper with parallel edges (adding-machine tape or ordinary unreinforced packaging gummed tape work well), designed to produce a regular convex p-gon. For the moment assume that we have a straight strip of paper that has creases or folds along straight lines emanating from vertices, which are equally spaced, at the top edge of the tape. Further assume that the creases at those vertices, labeled A_nk, on the top edge, form identical angles of p/p with the top edge, as shown in Figure 1(a). If we fold this strip on A_nkA_nk+2, as shown in Figure 1(b), and then twist the tape so that it folds on A_nkA_nk+1, as shown in Figure 1(c), the direction of the top edge of the tape will be rotated through an angle of 2p/p. We call this process of folding and twisting the FAT-algorithm.

Figure 1

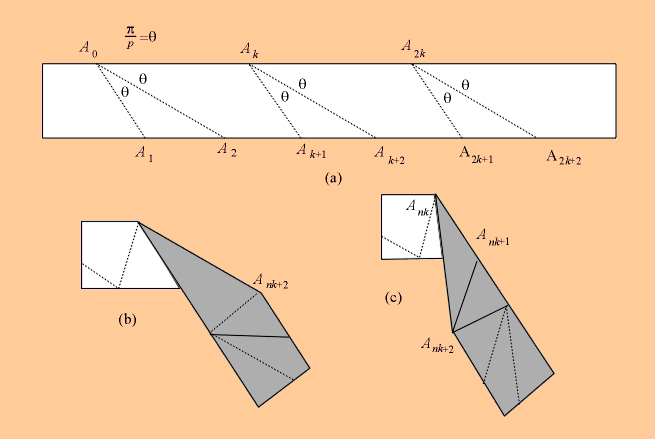
Now observe that if the FAT-algorithm is performed on a sequence of angles, each of which measures p/p, at the first p of a number of equally spaced locations along the top of the tape, in our case at A_nk for n = 0,1,2,...,p-1, then the top edge of the tape will have turned through an angle of 2p, so that the point A_pk will then be coincident with A₀. Thus the top edge of the tape visits every vertex of a regular convex p-gon, and thus itself describes a regular p-gon. A picture of the tape with its crease lines, and the resulting start of the construction of the regular p-gon, is given in Figure 2. Notice that we have not adhered there to our systematic enumeration of the vertices on the two edges of the tape that play a role in the construction. (The enumeration has served its purpose!)

Notice, too, that if we had the strip of paper shown in Figure 2(a), with its crease lines, we could then introduce secondary crease lines bisecting each of the angles nearest the top edge of the tape and this tape could then be used to construct a regular 2p-gon with the FAT-algorithm. We could then, in principle, repeat this secondary procedure, as often as we wished, to construct regular 4p-gons, 8p-gons,... It is for this reason that we only need to concern ourselves with devising primary folding procedures for regular polygons having an odd number of sides in order to be able to assure ourselves we can, indeed, fold all regular polygons.

Figure 2

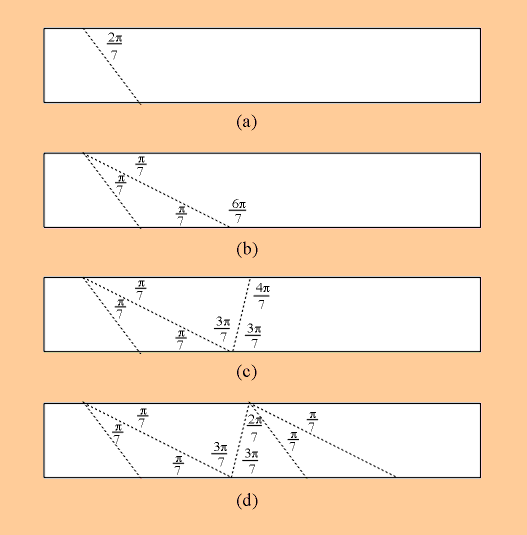
Figure 3

Now, since the regular convex 7-gon is the first polygon we encounter for which we do not have available a Euclidean construction, we are faced with a real difficulty in making available a crease line making an angle of p/7 with the top edge of the tape. We proceed by adopting a general policy, that we will eventually say more about - we call it our optimistic strategy. Assume that we can crease an angle of 2p/7 (certainly we can come close) as shown in Figure 3(a). Given that we have the angle of 2p/7, then simply folding the top edge of the strip DOWN to bisect this angle will produce two adjacent angles of p/7 at the top edge as shown in Figure 3(b). (We say that p/7 is the putative angle on this tape.) Then, since we are content with this arrangement, we go to the bottom of the tape, and now we really start the folding procedure.

We observe that the angle to the right of the last crease line is 6p/7 - and our policy, as paper folders, is that we always avoid leaving even multiples of p in the numerator of any angle next to the edge of the tape, so we bisect this angle of 6p/7, by bringing the bottom edge of the tape UP to coincide with the last crease line as shown in Figure 3(c). We settle for this (because we are content with an odd multiple of p in the numerator) and go to the top of the tape where we observe that the angle to the right of the last crease line is 4p/7 - and, in accordance with our stated policy, we bisect this angle twice, each time bringing the top edge of the tape DOWN to coincide with the lase crease line, obtaining the arrangement of crease lines shown in Figure 3(d). But now we notice something miraculous has occurred! If we had really started with an angle of exactly 2p/7, and if we now continue introducing crease lines by repeatedly folding the tape UP once at the bottom and DOWN twice at the top, we get precisely what we want; namely, pairs of adjacent angles, measuring p/7, at equally spaced intervals along the top edge of the tape. Let us call this folding procedure the U¹D²- or D²U¹-folding procedure and call the strip of creased paper it produces ² U¹D²- or D²U¹-tape.

We suggest that before reading further you get a piece of paper and fold an acute angle that you regard as a good approximation to 2p/7. Then fold about 40 triangles using the D²U¹-folding procedure just described, throw away the first 10 triangles, and try to construct the FAT 7-gon shown in Figure 4(b). You will have no doubt that what you have created is, in fact, a 7-gon, but you may wonder why it should have worked so well. In other words, how can we prove that this evident convergence must take place? One approach is to admit that the first angle folded down from the top of the tape in Figure 3(a) might not have been precisely 2p/7. Then the bisection forming the next crease would make two acute angles nearest the top edge in Figure 3(b) only approximately p/7; let us call them p/7+e (where e may be either positive or negative). Consequently the angle to the right of this crease, at the bottom of the tape, would measure 6p/7-e. When this angle is bisected, by folding up, the resulting acute angles nearest the bottom of the tape, labeled 3p/7 in Figure 3(c), would, in fact, measure 3p/7-e/2, forcing the angle to the right of this crease line at the top of the tape to have measure 4p/7+e/2. When this last angle is bisected twice by folding the tape down, the two acute angles nearest the top edge of the tape will measure p/7+p/2³. This makes it clear that every time we repeat a D²U¹-folding on the tape the error is reduced by a factor of 2³.

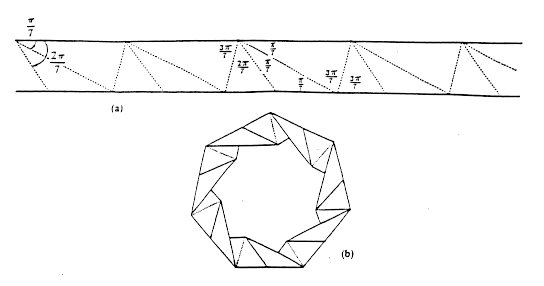
Figure 4

Now it should be clear how our optimistic strategy has paid off. By blandly assuming we have an angle of p/7 to begin with, and folding accordingly, we get what we want - successive angles at the top of the tape which, as we fold, rapidly get closer and closer to p/7! A truly remarkable vindication of our optimistic strategy!

In practice the approximations we obtain by folding paper are quite as accurate as the real world constructions with a straight edge and compass - for the latter are only perfect in the mind. In both cases the real world result is a function of human skill, but our procedure, unlike the Euclidean procedure, is very forgiving in that it tends to reduce the effects of human error - and, for many people, it is far easier to bisect an angle by folding paper than it is with a straight edge and compass.

Observe that it is in the nature of the folding procedure that we will always be folding DOWN a certain number of times at the top and then folding UP a certain (not necessarily the same) number of times at the bottom and then folding DOWN (possibly an entirely new) number of times at the top, etc. Indeed, a typical folding procedure may be represented by a sequence of exponents attached to the letters DUDUDUDU... the sequence stopping to avoid simply repeating a given finite string of exponents. The length of the repeat for the exponents is called the period of the folding procedure. (Thus the folding that produced the 7-gon is called a 2-period folding procedure.) It is an important fact that, for every odd p, a regular p-gon may be folded by instructions so encoded. It is thus very natural to ask what regular p-gons can be produced by the 2-period folding procedure?

In the process of answering this question we make straightforward use of the following:³

Lemma 2.1 For any three real numbers a, b and x₀, with a ¹ 0, let the sequence {x_k}, k = 0,1,2,... be defined by the recurrence relation

Then if |a| > 1, x_k ® b/(1+a) as k ® ¥.
Proof: Set x_k = b/(1+a) + y_k. Then y_k + ay_k+1 = 0. It follows that y_k = ((-1)/a)^ky₀.

If |a| > 1, ((-1)/a)^k ® 0, so that y_k ® 0 as k ® ¥. Hence x_k ® b/(1+a) as k ® ¥. Notice that y_k is the error at the k^th stage, and that the absolute value of y_k is equal to |y₀|/|a|^k.

This result is the special linear case of the Contraction Mapping Principle (see [W]). We point out that it is significant that neither the convergence nor the limit depends on the initial value x₀. This implies, in terms of the folding, that the process will converge, and to the same limit, no matter how we fold the tape to produce the first line - this is what justifies our optimistic strategy! And, as we have seen in our example, and as we will soon demonstrate in general, the result of the lemma tells us that the convergence of our folding procedure is rapid, since in all cases |a| will be a positive power of 2.

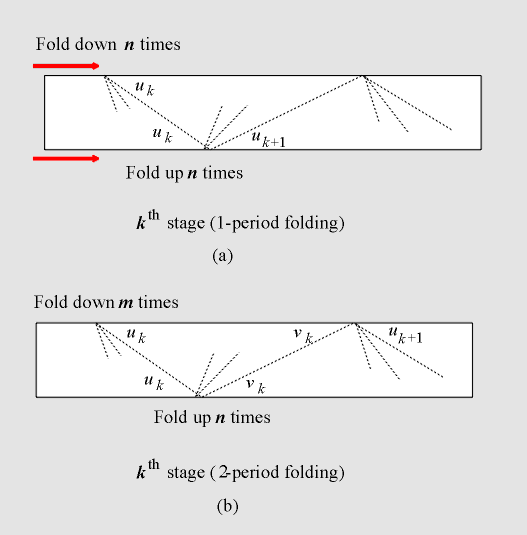
Figure 5

Now we will look at the general 2-period folding procedure, D^mUⁿ. In this case a typical portion of the tape would appear as shown in Figure 5(b). If the folding process had been started with an arbitrary angle u₀ at the top of the tape we would have, at the k^th stage,

and hence it follows that

Thus, using Lemma 2.1, we see that

as   k ® ¥, so that (2ⁿ-1)p/(2^m+n-1) is the putative angle ap/b. Thus the FAT-algorithm will produce, from this tape, a star {b/a}-gon, where the fraction b/a may turn out not to be reduced (for example when m = 4, n = 2), with a = 2ⁿ-1, b = 2^m+n-1. By symmetry we infer that

vk ® 2m-1 2m+n-1 p

as k ® ¥.

Furthermore, if we assume an initial error E₀ then we know that the error at the k^th stage (when folding D^mUⁿ has been done exactly k times) will be given by E_k = E₀/2^(m+n)k. Hence, we see that in the case of our D²U¹-folding (Figure 3) any initial error E₀ is, as we already saw from our initial argument, reduced by a factor of 2³ between consecutive states. It should now be clear why we advised throwing away the first part of the tape - but, likewise, it should also be clear that it is never necessary to throw away very much of the tape. In practice, convergence is very rapid indeed, and if one made it a rule of thumb always to throw away the first 20 crease lines on the tape for any iterative folding procedure, one would be absolutely safe.

We have seen that the D^mUⁿ-folding procedure, or, as we may more succinctly describe it, the (m,n)-folding procedure, produces angles p/s on the tape, where

s = 2m+n-1 2n-1        (2.2)

Notice that when n = m the folding becomes, technically, a 1-period folding procedure which produces a regular s-gon, where s = (2²ⁿ-1)/(2ⁿ-1) = 2ⁿ+1. Thus we see, immediately, that the DⁿUⁿ-folding will produce tape to which the FAT-algorithm can be applied to obtain regular (2ⁿ+1)-gons. These constructions provide approximations to many (but not all) of the polygons the Greeks and Gauss were able to construct with Euclidean tools. We can certainly construct a regular polygon whose number of sides is a Fermat number, but (see [Rec]) it is never possible to construct, with a 1-period folding those regular polygons where the number of sides is the product of at least two distinct Fermat numbers (thus, 15 serves as the first example where we find trouble).

The polygons which are of most interest to us in the construction of regular polyhedra are those with 3 or 5 sides (since we have exact constructions for the square). Our companion article [Rec] of this issue contains very explicit instructions of the folding procedures that produce the D¹U¹- and the D²U²-tape (which can be used to construct 3- and 5- gons, respectively) along with equally explicit instructions for building some braided polyhedra from the tape produced. The reader is encouraged to at least peruse that part of this issue before going on, since we will be making references to some of the models whose construction is described there in the next section.

Before we begin the discussion of symmetry let us finish explaining how you might construct those regular polygons that cannot be folded by the 1- or 2-period folding procedures. For example, suppose we wanted to construct a regular 11-gon. Our arguments in [HP1, 2 or 3] show that no 2-period (or 1-period) folding procedure can possibly produce an 11-gon.

In fact, the example of constructing the regular 11-gon is sufficiently general to show the construction of any regular p-gon, with p odd. So let us demonstrate how to construct a regular 11-gon. we proceed as we did in the construction of the regular 7-gon (in Section 2) - we adopt our optimistic strategy (which means that we assume we've got what we want and, as we will show, we then actually get what we want!). Thus we assume we can fold an angle of 2p/11. We bisect it by introducing a crease line, and follow the crease line to the bottom of the tape. The folding procedure now commences at the bottom of the tape. Thus

(1) Each new crease line goes in the forward (left to right) direction along the tape;

(2) Each new crease line always bisects the angle between the last crease line and the edge of the tape from which it emanates;

(3) The isection of angles at any vertex continues until a crease line produces an angle of the form ap/11 where a is an odd number; then the folding stops at that vertex and commences at the intersection point of the last crease line with the other edge of the tape.

Once again the optimistic strategy works and our procedure results in tape whose angles converge to those shown in Figure 6(b). We could then denote this folding procedure by U¹D¹U³D¹ U¹D³... interpreted in the obvious way on the tape - that is, the first exponent "1" refers to the one bisection (producing a line in the upward direction) at the vertices A_6n (for n = 0,1,2,...) on the bottom of the tape; similarly the next "1" refers to the bisection (producing a crease in the downward direction) made at the bottom of the tape through the vertices A_6n+1; etc. However, since the folding procedure is duplicated halfway through, we can abbreviate the notation and write simply {1,1,3}, with the understanding that we alternately fold from the bottom and top of the tape as described, with the number of bisections at each vertex running, in order, through the values 1, 1, 3,... We call this a primary folding procedure of period 3 or a 3-period folding, for obvious reasons. The crease lines made during this procedure are called primary crease lines.

Figure 6: (Note that the indexing of the vertices is not the same as that in Fig. 1).

Our argument, as described for p = 11, may clearly be applied to any odd number p. However, our tape for the 11-gon has a special symmetry as a consequence of its odd period; namely that if it is "flipped" about the horizontal line halfway between its parallel edges, the result is a translate of the original tape. As a practical matter this special symmetry of the tape means that we can use either the top edge or the bottom edge of the tape to construct our polygons. On tapes with an even period the top edge and the bottom edge of the tape are not translates of each other (under the horizontal flip), which simply means that care must be taken in choosing the edge of the tape used to construct a specific polygon.

A proof for the convergence for the general folding procedure may be given that is similar to the one we gave for the primary folding procedure of period 2, using Lemma 2.1. Alternatively one could revert to an error-type proof like that given for the 7-gon. We leave the details to the reader.

For further reading, and a discussion of the construction of star polygons see [HP2, 3 and 5].

---

² It is our habit to refer to D²U¹-tape, but this choice is quite arbitrary.
³ This lemma is actually applicable to folding procedures of arbitrary period.

---