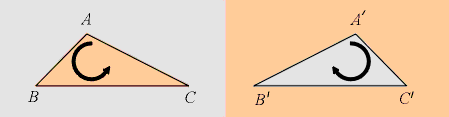
|
Figure 7: The triangle ABC may be transformed by
a rotation in 3 dimensions into the triangle A'B'C'
reversing the orientation of the triangle.
|
Example 3.2 We may 'step up a dimension', passing to the group
E3 of Euclidean motions in 3-dimensional space.
Notice that it is natural to
think of reflexions in a line (of a planar figure) as a 'motion' since it can
be achieved by a rotation in some suitable ambient 3-dimensional space
containing the plane figure. However, it requires a greater intellectual
effort to think of reflexion in a plane (of a spatial figure) as a motion in
some ambient 4-dimensional space! Who would think of turning the golden
dodecahedron (see Figure 8 of
[Rec]) inside out? Thus it is
common not to include such reflexions in defining 3-dimensional geometry.
This preference is, however, a consequence of our experience of living in a
3-dimensional world and has no mathematical basis. However, since, in
this article, and its companion article, we are highlighting the construction
of actual physical models of geometrical configurations, it is entirely
reasonable to omit 'motions' to which the models themselves cannot be
subjected.
We now introduce the key idea in the precise definition of symmetry. Let a
geometry be defined on the ambient space of a geometric configuration A
by means of the group of motions G. Then the symmetry group of A,
relative to the geometry defined by G, is the subgroup GA of
G consisting of those motions g Î G
such that Ag = A, that is, those motions which map A onto itself,
or, as we say, under which A is invariant. Thus, for example, if our geometry
is defined by rotations and translations in the plane, and if A is an equilateral
triangle, then its symmetry group GA consists of rotations about its
center through 0°, 120°,
and 240°; if, in our geometry, we also allow reflexions, then the
symmetry group has 6 elements instead of 3, and is, in fact, the
very well-known group S3, called the symmetric group on
3 symbols - the symbols may be thought of as the vertices of
the triangle. We must repeat for emphasis that the symmetry group GA
of the configuration A is a relative notion, depending on the choice of
'geometry' G.
It is plain that no compact (bounded) configuration can possibly be invariant
under a translation. Thus when we are considering the symmetry group of
such a figure we may suppose G to be generated by rotations and,
perhaps, reflexions. Moreover, any such motion in the plane is determined
by its effect on 3 independent points and any such motion in 3-dimensional space
is determined by its effect on 4 independent
points. Since a (plane) polygon has at least 3 vertices and a
polyhedron has at least 4 vertices, and since any element of the
symmetry group of a polygon or a polyhedron must map vertices to vertices, it
follows that the symmetry group of a polygon or a polyhedron is finite
(compare the symmetry groups of a circle or a sphere).
The symmetry group of any polygon with n sides is, by the argument
above, a subgroup of Sn, the group of permutations of
n symbols, also called the symmetric group on n symbols.
If G is generated by rotations alone, and the polygon is regular,
this group is the cyclic
group of order n, often written Cn, generated by a rotation
through an angle of 2p/n radians about the center of the
polygonal region. If G also includes reflexions, this group has 2n
elements and includes n reflexions; this group is called a
dihedral group and is often written Dn.
In discussing the symmetry groups of polyhedra, we will, as indicated above,
always assume that the geometry is given by the group G generated by
rotations in 3-dimensional space. Then the symmetry group of the
regular tetrahedron is the so-called alternating group A4. In
general, An is the subgroup of Sn consisting of the even
permutations of n symbols; it is of index 2 in Sn, that is,
its order is half that of Sn, or n!/2. Thus the
order of A4 is 12. The cube and the regular octahedron have the
same symmetry group, namely S4. It is easy to see why the symmetry
groups are the same; for the centers of the faces of a cube are the vertices
of a regular octahedron, and the centers of the faces of a regular octahedron
are the vertices of a cube. Likewise, and for the same reason, the regular
dodecahedron and the regular isocahedron have the same symmetry group, which
is A5. It is a matter of great interest and relevance here that the
symmetries of the Diagonal Cube and the special braided octahedron of
Figure 7 and Figure 16,
respectively (of [Rec]) each permute the four braided
strips from which the models are made. This provides a beautiful
explanation of why their symmetry group is the symmetry group S4.
We are now in a position to give at least one precise meaning to the
statement "Figure A is more symmetric than Figure B". If it
happens that the symmetry group GA of A strictly contains the
symmetry group GB of B, then we are surely entitled to say that
A is more symmetric than B. Notice that the situation described
may, in fact, occur because B is obtained from A by adding
features which destroy some of the symmetry of A. For example, the
coloring of the strips used to construct the braided Platonic solids of
Figure 6 of [Rec]
will reduce the symmetry in all cases but
that of the cube.
However, the definition above is really too restrictive. For we would like
to be able to say that the regular n-gon becomes more symmetric as n
increases. We are thus led to a weaker notion which will be useful
provided we are dealing with figures with finite symmetry groups (e.g.,
polygons and polyhedra). We could then say - and do say - that A
is more symmetric than B if GA has more elements than
GB. Thus we have, in fact, two notions whereby we may compare
symmetry - and they have the merit of being consistent. Indeed, if A is more
symmetric than B in the first sense, it is more symmetric than B
in the second sense - but not conversely.
Notice that we deliberately avoid the statement - often to be found in
popular writing - "A is a symmetric figure". We regard this statement as
having no precise meaning!