
|
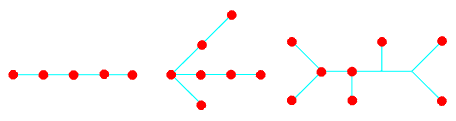
In his fundamental work "Classification des noeuds et des enlancements" (371 pages published only as a preprint) A.Caudron introduced the first classification of knots and links. Every initial link L is completely determined by the weighted graph GL, and all links are divided into several classes: "worlds", according to the types of the corresponding graphs. For example, a link L is rational if its graph GL is an interval, it belongs to the "stellar world" if its graph contains no cycles and has only one vertex of valence greater than 2, or to the "arborescent world" if its graph is a tree. |
|
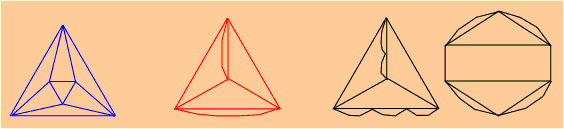
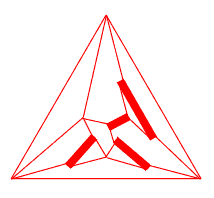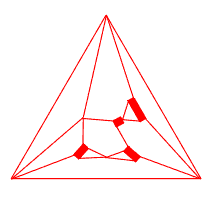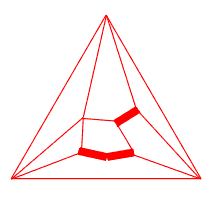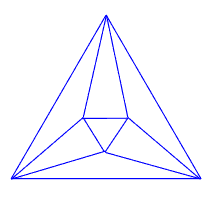
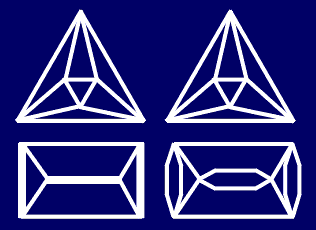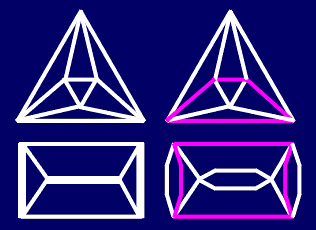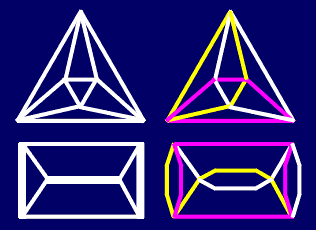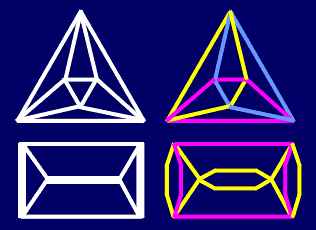
The origin of J.Conway and A.Caudron concept are the ideas of T.P.Kirkman, used for the exhaustive derivation and classification of link diagrams: systematical introduction of digons (called by him "flaps") and classification of link diagrams into solid, subsolid and unsolid ones. According to T.P.Kirkman, solid link (or basic polyhedron in Conway terms) is a diagram containing no digons, a subsolid link (or generating link in the present paper) is a diagram which admits no simple closed curve in the plane cutting it transversely in just two points (whether crossing points or distinct edges), except through the two crossings of a digon; any other diagram is unsolid. |
|
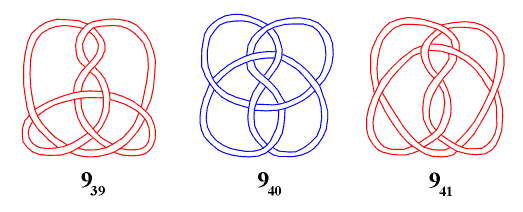
From T.P.Kirkman's classification principle in the existing knot tables remained just one memory: solid knots (or basic polyhedra) are at the end of the tables. But even this rule is sometimes disturbed: basic polyhedron 9* - "solid" knot 940 is placed between "subsolid" knots 939 (2:2:20) and 941 (20:20:20) derived both from the basic polyhedron 6*. |
|
As the opposite transformation to the systematical introduction of digons, T.P.Kirkman used as a principal transformation in the reduction process the removal of digons. This way, every link collapses into an irreducible diagram: a solid link. The same idea used by J.Conway was improved by A.Caudron, so his "worlds" correspond to the different "levels of collapsing", connected with the mentioned graph properties. |
|
From weighted or any other graphs corrsponding to links, at first glance it is not possible to make any conclusion about the number of components. It represents the secondary property of every link, so in every subdivision of links according to the number of components was lost the original ordering principle, unrecognizable in the subsets obtained: knots, 2-component, 3-component links, etc. This holds even in the case of A.Caudron paper, where the possibilities for the classification based on the partition theory, and for some combinatorial results remained unexplored. |