34Kb

Amphicheiral knots with n = 12 crossings are derived by M.Hasseman [47]. After the correction for the knot 10. 26 and identification of 7 duplications [48], their complete list that consists of 54 knots, given by Conway symbols showing their (anti)symmetry, is the following:

01. 62
02. 5125
03. (3,3)2
04. 321123
05. 34
06. (21,21)2
07. 312213
08. 221422
09. 2182
10. 26
11. 4224
12. 21212212
13. (211,2)2
14. (3,2+)2
15. (21,2+)2

16 = 13
17. (22,2)2
18. 2422
19. 2.2.2.2.20.20
20. 20.21.21.20
21. 2.2.20.2.2.20
22. 12L
23. 10**:20::.20
24. 10*20:::20
25. 8*.20:2.2:20
26. 8*2.2.2.2
27. 2.21.21.2
28. .21.21.2.2
29. 3.2.2.3
30. .3.3.2.2

31. 12K
32. 8*2.20.20.2
33. 8*.21.21
34. 8*2.2:.20.20
35. 10**20::.20
36 = 20
37. 8*210:.210
38. .4.4
39. .31.31
40. 8*20.20:.20.20
41. 8*3.3
42. 8*30.30
43. 10*2::.2
44. 10**:2::.2
45. 10**2::.2

46. 8*20.20.20.20
47. 30.2.2.30
48. 8*3:.3
49. 8*30:.30
50. .22.22
51 = 50
52. .3.3.20.20
53. 10**2::::2
54 = 40
55. 10**:20.20
56. 10**:2.2
57 = 45
58. 12B
59. .21.2.210.20
60 = 59
61 = 6



4Kb

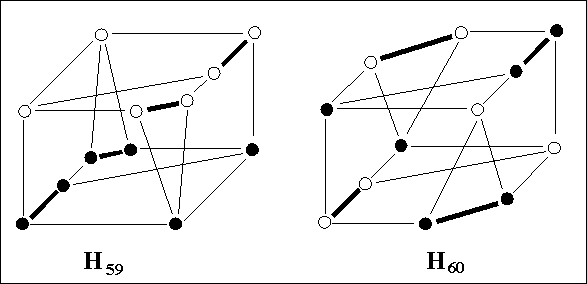
Amphicheiral knot H59=H60 and two of its vertex-antisymmetrical 3D-presentations, based on the antiinversion.



8Kb

Even in the case when the polynomial d(t) and Liang polynomial are not able to recognize some concealed antisymmetry, it could be seen from the corresponding vertex-bicolored diagrams. For example, in the case of the 14-crossing amphicheiral knot for which the both polynomials failed, its amphicheirality could be explained by the presence of rotational antireflection, i.e. by geometrical antisymmetry arguments. Antisymmetrical knot diagrams, rigid and non-rigid achirality are considered by J.Liang & K.Mislow [22] and E.Flapan [29].